题目内容
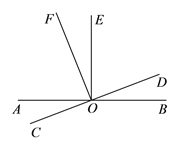
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
, ![]() .
.
(![]() )
)![]() 的余角是__________(填写所有符合要求的角).
的余角是__________(填写所有符合要求的角).
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
(3)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)∠BOD、∠EOF、∠AOC; (2)∠BOF=110°;(3)∠COE=135°.
【解析】试题分析:(1)先求得∠BOE和∠FOD为直角,然后依据余角的性质、对顶角的性质进行解答即可;
(2)先依据余角的性质得到∠EOF的度数,然后再由∠BOF=∠FOE+∠EOB求解即可;
(3)先根据∠BOE=90°得出∠BOD+∠DOE=90°,由条件∠DOE=∠BOD可得∠DOE=∠BOD=45°,然后根据∠COE=180°-∠DOE计算即可得出答案.
试题解析:
解:(1)∵∠AOE=90°,
∴∠EOB=90°,
∴∠DOE与∠DOB互余.
∵∠AOC=∠DOB,
∴∠AOC与∠EOD互余.
∵∠COF=90°,
∴∠DOF=90°,
∴∠DOE与∠EOF互余.
故答案为:∠BOD、∠EOF、∠AOC;
(2)∵∠DOF =90°,即∠DOE+∠EOF=90°,
∴∠EOF=90°-∠DOE=90°-70°=20°,
∴∠BOF=∠EOF+∠EOB=20°+90°=110°;
(3)∵∠AOE=90°,∴∠BOE=180°-∠AOE=90°,即∠BOD+∠DOE=90°,
∵∠DOE=∠BOD,∴∠DOE=∠BOD=45°,
∴∠COE=180°-∠DOE=135°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目