题目内容
【题目】将矩形ABCD(如图)绕点A旋转后,点D落在对角线AC上的点D′,点C落到C′,如果AB=3,BC=4,那么CC′的长为
【答案】![]()
【解析】解:如图, 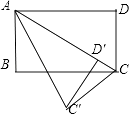
∵四边形ABCD为矩形,
∴∠B=∠D=90°,AD=BC=4;
由勾股定理得:
AC= ![]() =5;
=5;
由旋转变换的性质得:
∠AD′C′=∠D=90°,AC′=AC=5,
AD′=AD=4,D′C′=DC=3;
∴D′C=5﹣4=1;
由勾股定理得:C′C2=C′D′2+D′C2 ,
∴C′C= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目