Question

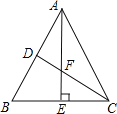
【题目】如图，在△ABC中，∠BAC=50°，∠B=60°，AE⊥BC于点E，CD平分∠ACB且分别与AB、AE交于点D、F，求∠AFC的度数．

Answer 1

【答案】125°

【解析】

试题分析:先根据垂直的定义求∠BAE的度数，再结合图形根据角的和差求出∠CAE的度数，利用三角形的内角和求∠ACB，因CD平分∠ACB，所以可得∠ACD，最后利用△AFC的内角和为180°，求得∠AFC的度数．

解：∵AE⊥BC，∴∠AEB=90°．

∵∠B=60°，

∴∠BAE=90°﹣60°=30°．

∴∠CAE=50°﹣30°=20°

∵∠BAC+∠B+∠ACB=180°，

∴∠ACB=180°﹣∠BAC﹣∠B=70°．

又∵CD平分∠ACB，

∴∠ACD=∠ACB=35°．

∴∠AFC=180°﹣35°﹣20°=125°．