题目内容
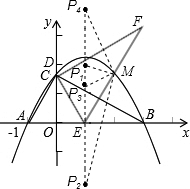
在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
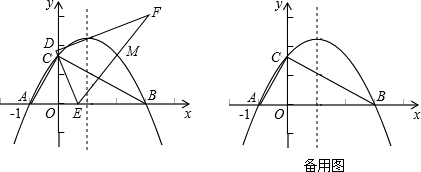
(1)请直接写出点B、C的坐标:B______、C______;并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
解:(1)∵点A(-1,0),
∴OA=1,
由图可知,∠BAC是三角板的60°角,∠ABC是30°角,
所以,OC=OA•tan60°=1× =
= ,
,
OB=OC•cot30°= ×
× =3,
=3,
所以,点B(3,0),C(0, ),
),
设抛物线解析式为y=ax2+bx+c,
则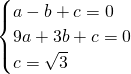 ,
,
解得 ,
,
所以,抛物线的解析式为y=- x2+
x2+ x+
x+ ;
;
(2)①∵△OCE∽△OBC,
∴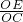 =
= ,
,
即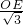 =
= ,
,
解得OE=1,
所以,AE=OA+OE=1+1=2,
即x=2时,△OCE∽△OBC;
②存在.理由如下:
抛物线的对称轴为x=- =-
=-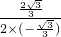 =1,
=1,
所以,点E为抛物线的对称轴与x轴的交点,
∵OA=OE,OC⊥x轴,∠BAC=60°,
∴△ACE是等边三角形,
∴∠AEC=60°,
又∠DEF=60°,
∴∠FEB=60°,
∴∠BAC=∠FEB,
∴EF∥AC,
由A(-1,0),C(0, )可得直线AC的解析式为y=
)可得直线AC的解析式为y= x+
x+ ,
,
∵点E(1,0),
∴直线EF的解析式为y= x-
x- ,
,
联立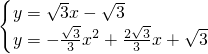 ,
,
解得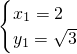 ,
, (舍去),
(舍去),
∴点M的坐标为(2, ),
),
EM= =2,
=2,
分三种情况讨论△PEM是等腰三角形,
当PE=EM时,PE=2,
所以,点P的坐标为(1,2)或(1,-2),
当PE=PM时,∵∠FEB=60°,
∴∠PEF=90°-60°=30°,
PE= EM÷cos30°=
EM÷cos30°= ×2÷
×2÷ =
= ,
,
所以,点P的坐标为(1, ),
),
当PM=EM时,PE=2EM•cos30°=2×2× =2
=2 ,
,
所以,点P的坐标为(1,2 ),
),
综上所述,抛物线对称轴上存在点P(1,2)或(1,-2)或(1, )或(1,2
)或(1,2 ),使△PEM是等腰三角形.
),使△PEM是等腰三角形.
分析:(1)利用解直角三角形求出OC的长度,再求出OB的长度,从而可得点B、C的坐标,然后利用待定系数法求二次函数解析式解答;
(2)①根据相似三角形对应边成比例列式求出OE的长度,再根据点A的坐标求出AO的长度,相加即可得到AE的长度,即x的值;
②根据①确定点E在对称轴上,然后求出∠FEB=60°,根据同位角相等两直线平行求出EF∥AC,再求出直线EF的解析式,与抛物线解析式联立求出点M的坐标,再利用两点间的距离公式求出EM的长度,再分PE=EM,PE=PM,PM=EM三种情况分别求解.
点评:本题是对二次函数的综合考查,主要涉及直角三角形的性质,待定系数法求二次函数解析式,相似三角形对应边成比例的性质,等腰三角形的性质,(2)②要根据等腰三角形腰的不同进行分情况讨论,根据题目图形,点M在x轴下方的情况可以舍去不予考虑.
∴OA=1,
由图可知,∠BAC是三角板的60°角,∠ABC是30°角,
所以,OC=OA•tan60°=1×
 =
= ,
,OB=OC•cot30°=
 ×
× =3,
=3,所以,点B(3,0),C(0,
 ),
),设抛物线解析式为y=ax2+bx+c,
则
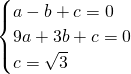 ,
,解得
 ,
,所以,抛物线的解析式为y=-
 x2+
x2+ x+
x+ ;
;(2)①∵△OCE∽△OBC,
∴
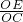 =
= ,
,即
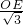 =
= ,
,解得OE=1,
所以,AE=OA+OE=1+1=2,
即x=2时,△OCE∽△OBC;
②存在.理由如下:
抛物线的对称轴为x=-
 =-
=-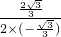 =1,
=1,所以,点E为抛物线的对称轴与x轴的交点,
∵OA=OE,OC⊥x轴,∠BAC=60°,
∴△ACE是等边三角形,
∴∠AEC=60°,
又∠DEF=60°,
∴∠FEB=60°,
∴∠BAC=∠FEB,
∴EF∥AC,
由A(-1,0),C(0,
 )可得直线AC的解析式为y=
)可得直线AC的解析式为y= x+
x+ ,
,∵点E(1,0),
∴直线EF的解析式为y=
 x-
x- ,
,联立
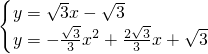 ,
,
解得
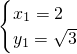 ,
, (舍去),
(舍去),∴点M的坐标为(2,
 ),
),EM=
 =2,
=2,分三种情况讨论△PEM是等腰三角形,
当PE=EM时,PE=2,
所以,点P的坐标为(1,2)或(1,-2),
当PE=PM时,∵∠FEB=60°,
∴∠PEF=90°-60°=30°,
PE=
 EM÷cos30°=
EM÷cos30°= ×2÷
×2÷ =
= ,
,所以,点P的坐标为(1,
 ),
),当PM=EM时,PE=2EM•cos30°=2×2×
 =2
=2 ,
,所以,点P的坐标为(1,2
 ),
),综上所述,抛物线对称轴上存在点P(1,2)或(1,-2)或(1,
 )或(1,2
)或(1,2 ),使△PEM是等腰三角形.
),使△PEM是等腰三角形.分析:(1)利用解直角三角形求出OC的长度,再求出OB的长度,从而可得点B、C的坐标,然后利用待定系数法求二次函数解析式解答;
(2)①根据相似三角形对应边成比例列式求出OE的长度,再根据点A的坐标求出AO的长度,相加即可得到AE的长度,即x的值;
②根据①确定点E在对称轴上,然后求出∠FEB=60°,根据同位角相等两直线平行求出EF∥AC,再求出直线EF的解析式,与抛物线解析式联立求出点M的坐标,再利用两点间的距离公式求出EM的长度,再分PE=EM,PE=PM,PM=EM三种情况分别求解.
点评:本题是对二次函数的综合考查,主要涉及直角三角形的性质,待定系数法求二次函数解析式,相似三角形对应边成比例的性质,等腰三角形的性质,(2)②要根据等腰三角形腰的不同进行分情况讨论,根据题目图形,点M在x轴下方的情况可以舍去不予考虑.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为