题目内容
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究: 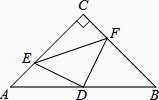
(1)求证:△DFE是等腰直角三角形;
(2)四边形CEDF的面积是否发生变化?若不变化,请求出面积.
【答案】
(1)解:连接CD,
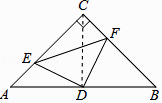
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB,
∵AE=CF,
在△ADE与△CDF中,
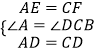 ,
,
∴△ADE≌△CDF,
∴DE=DF,∠CDF=∠ADE,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=∠EDF=90°,
∴DE⊥DF,
∴△DFE是等腰直角三角形;
(2)解:四边形CEDF的面积不发生变化.
理由:∵△ADE≌△CDF,
∴S△CDF=S△ADE
∴S四边形CEFD=S△ADC.
∴四边形CEDF的面积是为定值,
∴四边形CEDF的面积为 ![]() ×
× ![]() ×4×4=4
×4×4=4
【解析】(1)连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DF=DE.所以△DEF是等腰直角三角形;(2)由割补法可知四边形CDFE的面积保持不变,利用三角形的面积公式求出答案.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目