题目内容
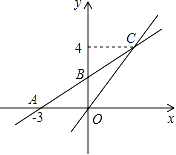
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为A（﹣3，0），与y轴交点为B，且与正比例函数y=
x的图象交于点C（m，4）．
（1）求m的值及一次函数y=kx+b的表达式；
（2）观察函数图象，直接写出关于x的不等式x＜kx+b的解集．
【答案】（1）一次函数的表达式为
；（2）x＜3
【解析】
（1）首先利用待定系数法把C（m，4）代入正比例函数y=
x中，计算出m的值，进而得到C点坐标，再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中，计算出k、b的值，进而得到一次函数解析式．
（2）根据函数图像直接写出答案即可．
（1）∵点C（m，4）在正比例函数y=
x的图象上，
∴
m，m=3即点C坐标为（3，4）．
∵一次函数 y=kx+b经过A（﹣3，0）、点C（3，4）
∴
，
解得：
，
∴一次函数的表达式为
；
（2）由图象可得不等式x＜kx+b的解为：x＜3
【题目】光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台，先将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区．两地区与该农机租赁公司商定的每天的租赁价格见表：
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），求y与x间的函数关系式，并写出x的取值范围；
（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元，说明有多少种分配方案，并将各种方案设计出来；
（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提一条合理化建议．
【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元． 经市场调研发现：该款工艺品每天的销售量y（件）与售价x（元）之间存在着如下表所示的一次函数关系．
售价x（元） | … | 70 | 90 | … |
销售量y（件） | … | 3000 | 1000 | … |
（利润=（售价﹣成本价）×销售量）
（1）求销售量y（件）与售价x（元）之间的函数关系式；
（2）你认为如何定价才能使工艺品厂每天获得的利润为40000元？
