题目内容
【题目】如图,在边长都为 a 的正方形内分别排列着一些大小相等的圆:
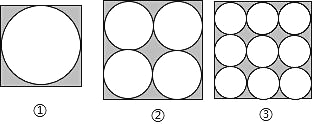
(1)根据图中的规律,第 4 个正方形内圆的个数是 ,第n 个正方形内圆的个数是_____.
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a 的代数式分别表示第 1 个正方形中、第 3 个正方形中阴影部分的面积(结果保留π);
②若 a=10,请直接写出第 2018 个正方形中阴影都分的面积 (结果保留π)
【答案】(1)16,n2(2)100﹣25π
【解析】
(1)观察上图可知第①个图形圆的个数是 12=1,第②个图形圆的个数是22=4,第③个图形圆的个数是 32=9,第④个图形圆的个数是 42=16,…,可知第 n 个正方形中圆的个数为 n2 个;
(2)阴影部分的面积等于正方形的面积减去圆的面积,由此列式后即可得到答案;从而推广运用得到结论.
(1)观察上图可知第①个图形圆的个数是12=1,
第②个图形圆的个数是22=4,
第③个图形圆的个数是32=9,
第④个图形圆的个数是42=16,
…,
可知第n个正方形中圆的个数为n2个;
故答案为:16,n2;
(2)①第一个S阴影=a2﹣π(![]() )2=
)2= ![]() a2;
a2;
第二个S阴影=a2﹣4π(![]() )2=
)2= ![]() a2;
a2;
第三个S阴影=a2﹣9π(![]() )2=
)2= ![]() a2;
a2;
②从以上计算看出三个图形中阴影部分的面积均相等,与圆的个数无关.
第n图形中阴影部分的面积是S阴影=a2﹣n2π(![]() )2=
)2= ![]() a2;
a2;
当 a=10,第 2018 个阴影部分的面积为![]() ×102=100﹣25π.
×102=100﹣25π.
故答案为:100﹣25π.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?