题目内容
【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
【答案】(1)直线AB的解析式为y=2x+8;(2)CD=![]() ;(3)满足题意的点E坐标为(0,5+
;(3)满足题意的点E坐标为(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() )或(0,5)或(0,
)或(0,5)或(0,![]() ).
).
【解析】
(1)用待定系数法求解即可;
(2)先由勾股定理求出AB的长,再由垂直平分线的性质求出AC的长,然后证明△CAD∽△OAB,利用相似三角形的对应边成比例即可求出CD的长,
(3)先由△CAD∽△OAB,求出AD和OD的长,然后分当CD=DE时,当CD=CE时,当CE=DE时三种情况求解即可;
(1)∵A(0,8),
∴设直线AB的解析式为y=kx+8,
∵B(﹣4,0),
∴﹣4k+8=0,
∴k=2,
∴直线AB的解析式为y=2x+8;
(2)∵A(0,8),B(﹣4,0),
∴OA=8,OB=4,AB=4![]() ,
,
∵CD是AB的垂直平分线,
∴∠ACD=90°,AC=![]() AB=2
AB=2![]() ,
,
∵∠ACD=∠AOB=90°,∠CAD=∠OAB,
∴△CAD∽△OAB,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ,
,
(3)∵△CAD∽△OAB,
∴![]() ,
,
∴![]() ,
,
∴AD=5,
∴OD=OA﹣AD=3,D(0,3),
当CD=DE时,DE=![]() ,
,
∴E(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() ),
),
当CD=CE时,如图1,
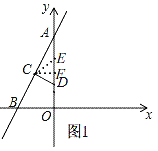
∵A(0,8),B(﹣4,0),
∴C(﹣2,4),
过点C作CF⊥y轴于F,
∴DF=EF,F(0,4),
∴E(0,5);
当CE=DE时,如图2,过E作E'G⊥CD,则E'G是线段CD的中垂线,

∵AB⊥CD,
∴E'G是△ACD的中位线,
∴DE'=AE'=![]() AD=
AD=![]() ,
,
∴OE'=OD+DE'=![]() ,
,
∴E(0,![]() ),
),
即:满足题意的点E坐标为(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() )或(0,5)或(0,
)或(0,5)或(0,![]() ).
).