题目内容
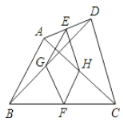
【题目】已知点![]() 与点
与点![]() ,
,![]() ,
,![]() 是一平行四边形的四个顶点,则
是一平行四边形的四个顶点,则![]() 长的最小值是( )
长的最小值是( )
A.10B.![]() C.
C.![]() D.9
D.9
【答案】C
【解析】
①CD是平行四边形的一条边,那么有AB=CD;②CD是平行四边形的一条对角线,过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,证△DBN≌△CAM,推出DN=CM=a-2,BN=AM=8a,得出D(10a,6+a),由勾股定理得:CD2=(10aa)2+(6+a+a-2)2=8a224a+116=8(a![]() )2+98,求出即可.
)2+98,求出即可.
有两种情况:
①CD是平行四边形的一条边,那么有AB=CD=![]() =10
=10
②CD是平行四边形的一条对角线,
过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,

则∠BND=∠DFA=∠CMA=∠QFA=90![]() ,
,
∠CAM+∠FQA=90![]() ,∠BDN+∠DBN=90
,∠BDN+∠DBN=90![]() ,
,
∵四边形ACBD是平行四边形,
∴BD=AC,∠C=∠D,BD∥AC,
∴∠BDF=∠FQA,
∴∠DBN=∠CAM,
∵在△DBN和△CAM中
 ,
,
∴△DBN≌△CAM(AAS),
∴DN=CM=a-2,BN=AM=8a,
D(10a,6+a),
由勾股定理得:CD2=(10aa)2+(6+a+a-2)2=8a224a+116=8(a![]() )2+98,
)2+98,
当a=![]() 时,CD有最小值,是
时,CD有最小值,是![]() =
=![]() ,
,
∵![]() <10,
<10,
∴CD的最小值是![]() .
.
故选:C.

练习册系列答案
相关题目