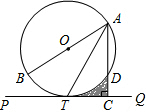
题目内容
如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E．
（1）求证：DE为⊙O的切线；
（2）若∠BAC=60°，CE=3，则⊙O的半径是多少？
（1）求证：DE为⊙O的切线；
（2）若∠BAC=60°，CE=3，则⊙O的半径是多少？
（1）证明：如图，连接OD，
∵AO=BO，BD=CD，
∴OD为△ACB的中位线，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∴DE是⊙O的切线；
（2）∵AB为⊙O的直径，
∴∠ADB=90°，
∴AD⊥BC，
又∴BD=CD，
∴△ABC为等腰三角形，
∵∠BAC=60°，
∴△ABC为等边三角形，
∴∠C=60°，AB=BC，
∴∠CDE=30°，
在Rt△CED中，
∵CE=3，∠CDE=30°，
∴CD=BD=6，
∴AB=12，
∴AO=6，即⊙O的半径等于6．
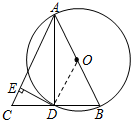
∵AO=BO，BD=CD，
∴OD为△ACB的中位线，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∴DE是⊙O的切线；
（2）∵AB为⊙O的直径，
∴∠ADB=90°，
∴AD⊥BC，
又∴BD=CD，
∴△ABC为等腰三角形，
∵∠BAC=60°，
∴△ABC为等边三角形，
∴∠C=60°，AB=BC，
∴∠CDE=30°，
在Rt△CED中，
∵CE=3，∠CDE=30°，
∴CD=BD=6，
∴AB=12，
∴AO=6，即⊙O的半径等于6．
练习册系列答案
相关题目
关于x的函数解析式（要指出函数的定义域）
P，连接PC，交AD于点E．
过点D作DF⊥OE交EC于点F．
