题目内容
如图,在△OAB中,C是AB的中点,反比例函数y=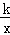 (k>0)在第一象限的图象经过A、C两点,若△OAB面积为6,则k的值为( )
(k>0)在第一象限的图象经过A、C两点,若△OAB面积为6,则k的值为( )
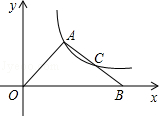
A.2 B.4 C.8 D.16
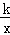 (k>0)在第一象限的图象经过A、C两点,若△OAB面积为6,则k的值为( )
(k>0)在第一象限的图象经过A、C两点,若△OAB面积为6,则k的值为( )
A.2 B.4 C.8 D.16
B
试题分析:分别过点A、点C作OB的垂线,垂足分别为点M、点N,根据C是AB的中点得到CN为△ADE的中位线,然后设MN=NB=a,CN=b,AM=2b,根据OM•AM=ON•CN,得到OM=a,最后根据面积=3a•2b÷2=3ab=6求得ab=2从而求得k=a•2b=2ab=4.
解:分别过点A、点C作OB的垂线,垂足分别为点M、点N,如图,
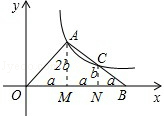
∵点C为AB的中点,
∴CN为△AMB的中位线,
∴MN=NB=a,CN=b,AM=2b,
∵又因为OM•AM=ON•CN
∴OM=a
∴这样面积=3a•2b÷2=3ab=6,
∴ab=2,
∴k=a•2b=2ab=4,
故选B.
点评:本题考查了反比例函数的比例系数的几何意义及三角形的中位线定理,解题的关键是正确的作出辅助线.

练习册系列答案
相关题目
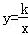 (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线 (k>0)的对径.
(k>0)的对径.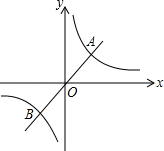
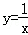 的对径;
的对径;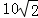 .求k的值.
.求k的值. 在第一象限相交,则k1、k2、k3的大小关系是 _________ .
在第一象限相交,则k1、k2、k3的大小关系是 _________ .
 的图象如图,则它关于x轴对称的图象的函数解析式为 y=﹣
的图象如图,则它关于x轴对称的图象的函数解析式为 y=﹣ (x>0) .
(x>0) .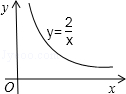
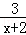 可以看作 和 成反比例.
可以看作 和 成反比例.
 的图象中,阴影部分的面积不等于4的是( )
的图象中,阴影部分的面积不等于4的是( )



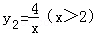 的图象如图所示,则下列结论正确的是( )
的图象如图所示,则下列结论正确的是( )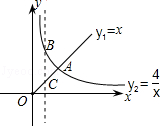
 的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是___________.
的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是___________.