题目内容
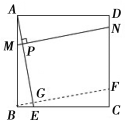
【题目】如图,直线![]() ∥
∥![]() ∥
∥![]() ,一等腰Rt△ABC的三个顶点A、B、C分别在直线
,一等腰Rt△ABC的三个顶点A、B、C分别在直线![]() 、
、![]() 、
、![]() 上,∠ACB=90°,AC交
上,∠ACB=90°,AC交![]() 于点D.若
于点D.若![]() 与
与![]() 的距离为1,
的距离为1,![]() 与
与![]() 的距离为4,则
的距离为4,则![]() 的值是( )
的值是( )
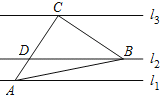
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先作出作BF⊥l3,AE⊥l3,再判断△ACE≌△CBF,求出CE=BF=3,CF=AE=4,然后由l2∥l3,求出DG,即可求出![]() 的值.
的值.
解:如图:作BF⊥l3,AE⊥l3,
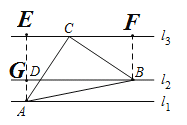
由题意,则AE=4,BF=4![]() 1=3,
1=3,
∵∠ACB=90°,
∴∠BCF+∠ACE=90°,
∵∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
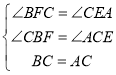 ,
,
∴△ACE≌△CBF;
∴CE=BF=3,CF=AE=4,
∴AG=1,BG=EF=CF+CE=7,
∴![]() ,
,
∵l2∥l3,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴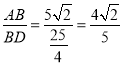 ;
;
故选:C.

练习册系列答案
相关题目
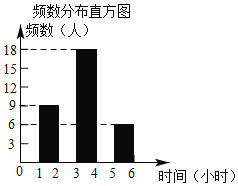
【题目】某中学兴趣小组为了解全校学生星期六和星期日在家使用手机的情况,兴趣小组随机抽取若干名学生,调查他们周末两天的使用手机时间,并根据调查结果绘制了下面两幅不完整的统计表和统计图.根据图表信息,解答下列问题:
阅读时间 (小时) | 频数 (人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= :
(2)将频数分布直方图补充完整;
(3)这个中学的学生共有1200人,根据上面信息来估算全校学生中周末两天使用手机时间不低于4小时的学生大约有多少人?