题目内容
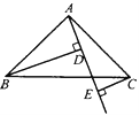
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
(1)AD与CE的大小关系如何?请说明理由;
(2)若BD=5,CE=2,求DE的长.
【答案】(1)AD=CE,理由见解析;(2)3.
【解析】
试题(1)利用角角边证出△ABD≌△CAE;得出BD=AE,AD=CE;
(2)证法同上,从而得出BD=DE+CE.
试题解析:(8分)(1)AD=CE
因为∠BAC=90°,BD⊥AE,所以∠ABD=∠CAE,
又因为AB=AC,∠ADB=∠AEC=90°,根据“AAS”可得△ABD≌△CAE,
所以AD=CE.
(2)因为△ABD≌△CAE,所以BD=AE,
所以DE=AE-AD=BD-CE=5-2=3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目