题目内容
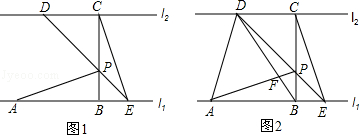
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当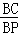 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当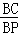 =n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求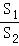 的值.
的值.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当
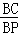 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;②当
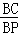 =n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求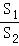 的值.
的值.
(1)证明见解析
?证明见解析
?n+1
?证明见解析
?n+1
试题分析:(1)由BC垂直于l1可得∠ABP=∠CBE,由SAS即可证明;
(2)①延长AP交CE于点H,由(1)及已知条件可得AP⊥CE,△CPD∽△BPE,从而有DP=PE,得出四边形BDCE是平行四边形,从而可得到CE//BD,问题得证;
②由已知条件分别用S表示出△PAD和△PCE的面积,代入即可.
试题解析:(1)∵BC⊥直线l1,
∴∠ABP=∠CBE,
在△ABP和△CBE中
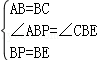
∴△ABP≌△CBE(SAS);
(2)①延长AP交CE于点H,
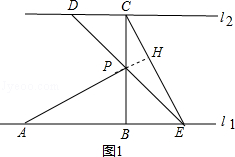
∵△ABP≌△CBE,
∴∠PAB=∠ECB,
∴∠PAB+∠AEE=∠ECB+∠AEH=90°,
∴AP⊥CE,
∵
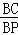 =2,即P为BC的中点,直线l1//直线l2,
=2,即P为BC的中点,直线l1//直线l2,∴△CPD∽△BPE,
∴
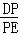 =
=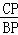 =
= ,
,∴DP=PE,
∴四边形BDCE是平行四边形,
∴CE//BD,
∵AP⊥CE,
∴AP⊥BD;
②∵
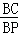 =N
=N∴BC=n•BP,
∴CP=(n﹣1)•BP,
∵CD//BE,
∴△CPD∽△BPE,
∴
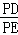 =
=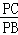 =n﹣1,
=n﹣1,即S2=(n﹣1)S,
∵S△PAB=S△BCE=n•S,
∴S△PAE=(n+1)•S,
∵
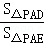 =
=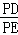 =n﹣1,
=n﹣1,∴S1=(n+1)(n﹣1)•S,
∴
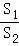 =
=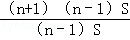 =n+1.
=n+1.
练习册系列答案
相关题目
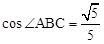 时,求AF及BE的长.
时,求AF及BE的长.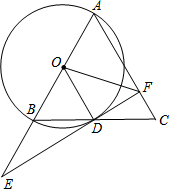
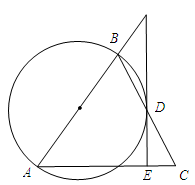
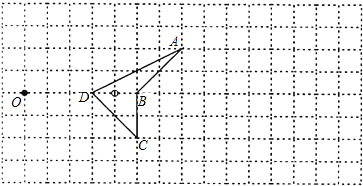





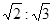
 CE时,EP+BP=__________.
CE时,EP+BP=__________.