题目内容
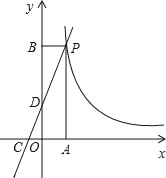
【题目】如图，一次函数y＝kx+2的图象与反比例函数y＝
的图象在第一象限的交点于P，函数y＝kx+2的图象分别交x轴、y轴于点C、D，已知△OCD的面积S△OCD＝1，OA＝2OC
（1）点D的坐标为 ；
（2）求一次函数解析式及m的值；
（3）写出当x＞0时，不等式kx+2＞的解集．
【答案】（1）（0，2）（2）12（3）x＞2
【解析】
（1）利用y轴上的点的坐标特征，利用解析式y＝kx+2确定D点坐标；
（2）利用S△OCD＝1求出OC的长得到C点坐标，则把C点坐标代入y＝kx+2求出k得到一次函数解析式；再利用一次函数解析式求出P点坐标，然后利用反比例函数图象上点的坐标特征求出m的值；
（3）在第一象限内，写出一次函数图象再反比例函数图象上方所对应的自变量的范围即可．
解:（1）当x＝0时，y＝kx+2＝2，则D（0，2），
故答案为（0，2）；
（2）∵S△OCD＝1，
∴
ODOC＝1，
∴OC＝1，
∴C（﹣1，0），
把C（﹣1，0）代入y＝kx+2得﹣k+2＝0，解得k＝2，
∴一次函数解析式为y＝2x+2；
∵OA＝2OC＝2，
∴P点的横坐标为2，
当x＝2时，y＝2x+2＝6，
∴P（2，6），
把P（2，6）代入y＝
，
∴m＝2×6＝12；
（3）不等式kx+2＞的解集为x＞2．
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟） | 里程数（公里） | 车费（元） | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
