题目内容
【题目】推理填空：
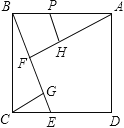
如图，直线AB，CD被直线EF所截，AD是∠CAB的角平分线，若∠3=∠1，∠2=50°，求∠4的度数．
解：∵直线AB与直线EF相交，
∴∠2=∠CAB=50°．（ ）
∵AD是∠CAB的角平分线，
∴∠1=∠5=
∠CAB=25°，（ ）
∵∠3=∠1，（已知）
∴∠3=25°，（等量代换）
∴∠3=∠5，（等量代换）
∴_______．（ ）
∵CD∥AB，（ ）
∴_______．（两直线平行，同位角相等）
【答案】对顶角相等；角平分线定义；CD∥AB；内错角相等，两直线平行；已证；∠4=∠2=50°
【解析】
根据平行线的判定及性质求角的过程，一步步把求解的过程补充完整即可．
直线AB与直线EF相交，
∴∠2=∠CAB=50°（对顶角相等），
∵AD是∠CAB的角平分线，
∴∠1=∠DAB=
∠CAB=25°（角平分线的定义），
∵∠3=∠1，（已知）
∴∠3=25°，（等量代换）
∴∠3=∠5，（等量代换）
∴CD∥AB．（ 内错角相等，两直线平行）
∵CD∥AB，（ 已证）
∴∠4=∠2=50°．（两直线平行，同位角相等）
故答案为：对顶角相等；角平分线定义；CD∥AB，内错角相等，两直线平行；已证；∠4=∠2=50°．
练习册系列答案
相关题目
