题目内容
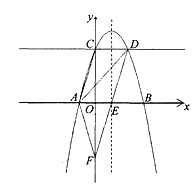
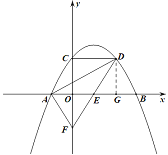
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?

【答案】(1)点A(﹣1,0),点B(3,0);(2)四边形ACDE是平行四边形.证明见解析;(3)当![]() 或
或![]() 时,△ADF为直角三角形.
时,△ADF为直角三角形.
【解析】
(1)根据抛物线的解析式可知当y=0时,x=﹣1或x=3,即可得解;
(2)由(1)可得抛物线对称轴为直线x=1,根据抛物线图象性质易得AE=CD=2,又因为![]() ,所以四边形ACDE是平行四边形;
,所以四边形ACDE是平行四边形;
(3)过点D作DG⊥AB于点G,通过“角边角”易证△OEF ≌△DEG,OF=GD=3a,即F点坐标为(0,-3a),①若∠DAF=90°,则∠DAG+∠FAO=90°,然后证明△AOF∽△DGA,得到![]() ,然后求得符合题意的a即可;②若∠DFA=90°,则∠DFC+∠AFO=90°,易得OF垂直平分AE,AF=EF,则∠DFC=∠AFO=45°,所以OF=OA,即
,然后求得符合题意的a即可;②若∠DFA=90°,则∠DFC+∠AFO=90°,易得OF垂直平分AE,AF=EF,则∠DFC=∠AFO=45°,所以OF=OA,即![]() ,a=
,a=![]() .
.
解(1)根据题意可知,
∵y=﹣a(x+1)(x﹣3),
∴当y=0时,x=﹣1或x=3,
∴点A(﹣1,0),点B(3,0);
(2)四边形ACDE是平行四边形.
证明如下:令![]() ,得
,得![]() ,即
,即![]() ,
,
∵点A(﹣1,0),B(3,0),
∴抛物线的对称轴为直线x=1,
∴点D(2,3a),E(1,0),
∴AE=CD=2,
又![]() ,
,
∴四边形ACDE是平行四边形;
(3)过点D作DG⊥AB于点G,由![]() ,可知OE=GE,
,可知OE=GE,
又∵∠FOE=∠DGE=90°,∠OEF=∠GED,
∴△OEF ≌△DEG(ASA),
∴OF=GD=3a,
∴F点坐标为(0,-3a),
讨论:①若∠DAF=90°,则∠DAG+∠FAO=90°,
又∠FAO+∠AFO=90°,
∴∠DAG=∠AFO,
又∠AOF=∠DGA=90°,
∴△AOF∽△DGA,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∵a > 0,
∴![]() ,
,
∵以上各步均可逆,故![]() 合题意;
合题意;
②若∠DFA=90°,则∠DFC+∠AFO=90°,
又∵![]() ,
,
∴OF垂直平分AE,
∴AF=EF,
∴∠DFC=∠AFO=45°,
∴OF=OA,
∴![]() ,
,
∴![]() ,
,
∵以上各步均可逆,故![]() 合题意.
合题意.
综上,当![]() 或
或![]() 时,△ADF为直角三角形.
时,△ADF为直角三角形.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案