题目内容
如图,在△ABC与△DEF中,点G、H分别是边BC、EF的中点,已知AB=2DE,AC=2DF,∠BAC=∠EDF.(1)中线AG与DH的比是多少?
(2)若△ABC的面积为8,则△DHF的面积是多少?
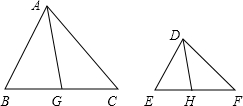
分析:(1)根据已知条件可以判定△ABC∽△DEF,然后由相似三角形的对应边成比例求得相似比是2,然后求得中线AG与DH的比;
(2)根据相似三角形的面积比等于相似比的平方求得△DEF的面积,然后利用△DEF与△DHF间的关系求△DHF的面积.
(2)根据相似三角形的面积比等于相似比的平方求得△DEF的面积,然后利用△DEF与△DHF间的关系求△DHF的面积.
解答:解:(1)∵AB=2DE,AC=2DF,
∴
=
=2,
又由∠BAC=∠EDF,
∴△ABC∽△DEF(SAS),
∴
=2;
(2)由(1)知△ABC∽△DEF,
=
=2,
∴S△ABC:S△DEF=4:1,
∴S△ABC=4S△DEF,
又∵S△DEF=2S△DHF,S△ABC=8,
∴S△ABC=8S△DHF=8,
∴S△DHF=1.即△DHF的面积是1.

∴
| AB |
| DE |
| AC |
| DF |
又由∠BAC=∠EDF,
∴△ABC∽△DEF(SAS),
∴
| AG |
| DH |
(2)由(1)知△ABC∽△DEF,
| AB |
| DE |
| AC |
| DF |
∴S△ABC:S△DEF=4:1,
∴S△ABC=4S△DEF,
又∵S△DEF=2S△DHF,S△ABC=8,
∴S△ABC=8S△DHF=8,
∴S△DHF=1.即△DHF的面积是1.

点评:本题考查了相似三角形的判定与性质.解得该题的关键是根据已知条件“AB=2DE,AC=2DF”求得△ABC和△DEF的对应边成比例,然后再由已知条件∠BAC=∠EDF证明△ABC∽△DEF.

练习册系列答案
相关题目
 34、如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在一条直线上,添加一个条件
34、如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在一条直线上,添加一个条件 6、如图,在△ABC与△BCD中,AB=AC=4,BD交AC于E点,AE=3,且∠BAC=2∠BDC.则BE•ED=
6、如图,在△ABC与△BCD中,AB=AC=4,BD交AC于E点,AE=3,且∠BAC=2∠BDC.则BE•ED=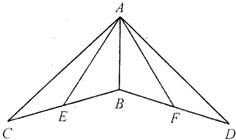 19、如图,在△ABC与△ABD中,BC=BD,∠ABC=∠ABD.点E为BC中点,点F为BD中点,连接AE,AF
19、如图,在△ABC与△ABD中,BC=BD,∠ABC=∠ABD.点E为BC中点,点F为BD中点,连接AE,AF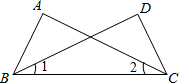 如图,在△ABC与△DCB中,∠1=∠2,增加一个条件后,不能使△ABC≌△DCB的是( )
如图,在△ABC与△DCB中,∠1=∠2,增加一个条件后,不能使△ABC≌△DCB的是( )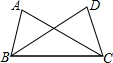 如图,在△ABC与△DCB中,∠A=∠D,要使△ABC≌△DCB,需要添加的一个条件是
如图,在△ABC与△DCB中,∠A=∠D,要使△ABC≌△DCB,需要添加的一个条件是