��Ŀ����
����Ŀ����ͼ��������A��0����4����������y= ![]() x2+bx+c��x���ཻ�ڵ�B����1��0����C��OΪ����ԭ�㣮
x2+bx+c��x���ཻ�ڵ�B����1��0����C��OΪ����ԭ�㣮
��1���������ߵĽ���ʽ��
��2����������y= ![]() x2+bx+c����ƽ��
x2+bx+c����ƽ�� ![]() ����λ���ȣ�������ƽ��m��m��0������λ���ȣ��õ��������ߣ����������ߵĶ���P�ڡ�ABC�ڣ���m��ȡֵ��Χ��
����λ���ȣ�������ƽ��m��m��0������λ���ȣ��õ��������ߣ����������ߵĶ���P�ڡ�ABC�ڣ���m��ȡֵ��Χ��
��3����x���·���������ͼ�����x��Գƣ��õ��µĺ���ͼ��C����ֱ��y=x+k��ͼ��Cʼ����3�����㣬������������k��ȡֵ��Χ��
���𰸡�
��1��
�⣺�߾�����A��0����4����������y= ![]() x2+bx+c��x���ཻ�ڵ�B����1��0����
x2+bx+c��x���ཻ�ڵ�B����1��0����
��  ��
��
��  ��
��
�������߽���ʽΪy= ![]() x2��
x2�� ![]() x��4
x��4
��2��
�⣺�ɣ�1��֪�������߽���ʽΪy= ![]() x2��
x2�� ![]() x��4=
x��4= ![]() ��x2��7x����4=
��x2��7x����4= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
�������������ƽ�� ![]() ����λ���ȵ������ߵĽ���ʽΪy=
����λ���ȵ������ߵĽ���ʽΪy= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
������ƽ��m��m��0������λ���ȣ��õ���������y= ![]() ��x+m��
��x+m�� ![]() ��2��
��2�� ![]() ��
��
�������ߵĶ���P����m+ ![]() ����
���� ![]() ����
����
����������y= ![]() x2��
x2�� ![]() x��4����y=0��
x��4����y=0�� ![]() x2��
x2�� ![]() x��4=0�����x=��1��8��
x��4=0�����x=��1��8��
��B��8��0������A��0����4����B����1��0����
��ֱ��AB�Ľ���ʽΪy=��4x��4��ֱ��AC�Ľ���ʽΪy= ![]() x��4��
x��4��
������P��AB��ʱ���� ![]() =��4������m+
=��4������m+ ![]() ����4�����m=
����4�����m= ![]() ��
��
������P��AC��ʱ���� ![]() =
= ![]() ����m+
����m+ ![]() ����4�����m=
����4�����m= ![]() ��
��
�൱��P�ڡ�ABC��ʱ ![]() ��m��
��m�� ![]()
��3��
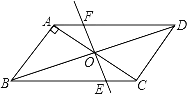
�⣺���ۺ�������ͼ����ͼ��ʾ��

ƽ��ֱ��y=x+k֪��ֱ��λ��l1��l2ʱ��������ͼ����������ͬ�Ĺ����㣮
�ٵ�ֱ��λ��l1ʱ����ʱl1����B����1��0����
��0=��1+k����k=1��
�ڡߵ�ֱ��λ��l2ʱ����ʱl2�뺯��y=�� ![]() x2+
x2+ ![]() x+4����1��x��8����ͼ����һ��������
x+4����1��x��8����ͼ����һ��������
���x+k=�� ![]() x2+
x2+ ![]() x+4����x2��5x��8+2k=0���������ʵ����
x+4����x2��5x��8+2k=0���������ʵ����
���=25��4��2k��8��=0����k= ![]() ��
��
����������k��ֵΪ1�� ![]()
����������1���������ߵĽ���ʽ��ֻ����������ϵ����ֻ�轫A��B����������뼴�ɵý⣮��2�����ȸ���ƽ��������ʾ���ƶ���ĺ�������ʽ��������m��ʾ���ú����Ķ������꣬�������ֱ��AB��AC�Ľ���ʽ�У�����ȷ��P�ڡ�ABC��ʱm��ȡֵ��Χ����3���ȸ��ݺ�������ʽ����ͼ�Σ�Ȼ����ͼ���ҳ���������x����������������Σ�������ֱ�ߵĽ���ʽ���Ӷ������m��ֵ��
�����㾫�������ն��κ�����ͼ��Ͷ��κ����������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��