��Ŀ����
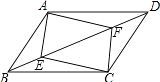
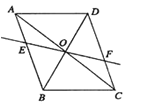
����Ŀ����1����ͼ����ƽ���ı���ABCD�У��Խ���AC,BD���ڵ�O��������O��ֱ�߽�AB��E����CD��F.��֤��OE��OF.
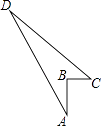
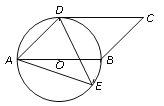
��2����ɳȺ�����ҹ����������������ҹ��Ϻ�����Ҫ����ɳij�����������в�����ҵ�����洬������A��ʱ���õ�λ�����������B����Ϊ�˷�ֹij��Ѳ�����ţ��������ҹ�C������ബǰ��B�����������C��AB�ľ���CDΪ20�����֪Aλ��C������ƫ��60�������ϣ�Bλ��C����ƫ��45���ķ����ϣ� ![]() ��1.7�������ȷ��1�����A��B֮��ľ���.
��1.7�������ȷ��1�����A��B֮��ľ���.
���𰸡���1��֤������������2��A��B��ľ�����(20![]() ��20)����
��20)����
�������������������1������ASA֤����OAE�ա�OCF���Ӷ��õ�OE��OF����2�����ݹ��ɶ������AD��BD�ľ��룬����AB��AD+BD�����AB֮��ľ��룻
���������
(1)֤�������ı���ABCD��ƽ���ı��Σ�
��OA��OC,AB��CD ��
���OAE����OCF
�ߡ�AOE����COF ��
���OAE�ա�OCF
��OE��OF
��2���⣺��CD��AB����ACD��600 ��
���A��300
��CD��20��
��AD��20![]()
��CD��AB, ��BCD��450��
���B��450 ��
��CD��BD��20
��AB�� AD�� BD��20![]() ��20(����)
��20(����)