题目内容
【题目】完成下面推理过程.在括号内的横线上填空或填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD
证明:∵AB∥EF
∴∠APE=()
∵EP⊥EQ
∴∠PEQ=()
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥()
∴AB∥CD()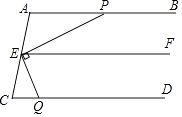
【答案】∠PEF;两直线平行,内错角相等;90°;垂直的定义;∠QEF;CD;内错角相等,两直线平行;平行公理
【解析】证明:∵AB∥EF∴∠APE=∠PEF(两直线平行,内错角相等)
∵EP⊥EQ
∴∠PEQ=90°(垂直的定义)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=∠QEF
∴EF∥CD(内错角相等,两直线平行)
∴AB∥CD(平行公理),
所以答案是:∠PEF,两直线平行,内错角相等,90°,∠QEF,内错角相等,两直线平行,CD,平行公理.
【考点精析】掌握垂线的性质和平行线的判定与性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目