题目内容
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
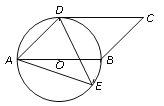
【答案】(1)CD与圆O相切,证明见解析;(2)AE=5 .
【解析】(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥CD,从而得出∠CDO=90°,即可证出答案.
(2)连接BE,则∠ADE=∠ABE,根据题意得sin∠ABE=![]() . 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
. 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
解:(1)CD与圆O相切. 证明:连接OD,则∠AOD=2∠AED =2×450=900.
∵四边形ABCD是平行四边形,∴AB//DC.∴∠CDO=∠AOD=90°.∴OD⊥CD. ∴CD与圆O相切
(2)连接BE,则∠ADE=∠ABE. ∴sin∠ADE=sin∠ABE=![]() .
.
∵AB是圆O的直径,∴∠AEB=900,AB=2×3=6.
在Rt△ABE中,sin∠ABE=![]() .∴AE=5 .
.∴AE=5 .
“点睛”此题考查了切线的判定、圆周角定理、垂线定理、平行四边形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用.

练习册系列答案
相关题目