题目内容

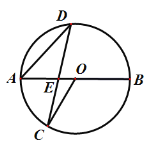
【题目】已知：如图，OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AB相交于点D，连结OD并延长交⊙O于点E，连结AE．

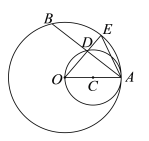
（1）求证：AD=DB．

（2）若AO=10，DE=4，求AE的长．

【答案】（1）见解析；（2）AE=4.

【解析】

（1）由OA是⊙C的直径知OD⊥AB，在⊙O中依据垂径定理可得；
（2）在Rt△ADO中求得AD=8，再在Rt△ADE中利用勾股定理可得答案．

（1）∵ OA是⊙C的直径

∴∠ADO=90°

∵ O是⊙O的圆心 ∠ADO=90°

∴AD=DB

（2）∵ ∠ADO=90°

∴OD+AD=AO

∵ OE=AO=10，DE=4，

∴OD=OE-DE=6

∴AD=8

∵ 在Rt△ADE中DE+AD=AE

∴AE=

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.

（1）求证：△AEF≌△DEB;

（2）求证：四边形ADCF是菱形.

【题目】如图，一个半径为2的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是

A.B.－2C.－D.2－

【题目】已知关于x的一元二次方程 kx2＋(2k＋1)x＋k＋2＝0．

（1）若该方程有两个不相等的实数根，求k的取值范围；

（2）若该方程的两根x1、x2满足＝－3，求k的值．

【题目】如图，AB是⊙O的直径，OC是⊙O的半径，点D是半圆AB上一动点（不与A、B重合）,连结DC交直径AB与点E,若∠AOC=60°，则∠AED的范围为（ ）

A.0°< ∠AED <180°B.30°< ∠AED <120°

C.60°< ∠AED <120°D.60°< ∠AED <150°

【题目】如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E．

（1）求证：△ABM ∽△EMA；

（2）若AB＝2，BM＝1，求DE的长．

【题目】已知关于的方程．

（1）若该方程有两个相等的实数根，求的值；

（2）求证：不论为何值，该方程一定有一个实数根是2；

（3）若、是该方程的两个根，且，求的值．

【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

（1）在图1中证明CE=CF；

（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．

【题目】如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB交⊙O于点H，E是BC上的一点，且BE＝BF，连接DE．

（1）求证：DE是⊙O的切线．

（2）若BF＝2，BD＝2，求⊙O的半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网