Question

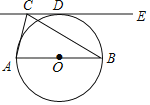
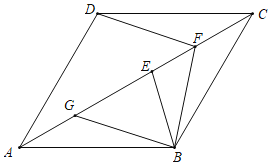
【题目】如图，将半径为4的沿弦折叠，圆上点折叠后恰好与圆点重合，连接并延长交于点，连接.点为弧上一点，、分别为线段、上一动点，则周长的最小值为___________.

Answer 1

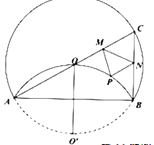
【答案】

【解析】

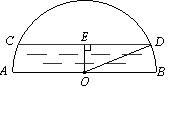
如图，首先求出∠ACB＝60°，作P关于AC、BC的对称点G、S，连接GS交AC、BC于M、N，可得 的周长＝GS，由中位线定理可得EF＝ GS，证明C、E、P、F四点共圆，根据∠ECF＝60°求出EF＝ CP，可得当CP取最小值时，EF取最小值，此时GS取最小值，即 的周长取最小值，连接PC、PO’、CO’，可得当P、K重合时CP取最小值，解直角△AO’C求出CO’，进而可得CP的最小值，然后由已证得的等量关系可得答案.

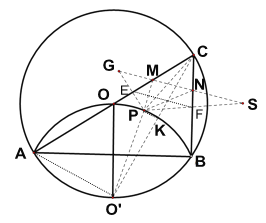
解：如图：连接AO’，

由折叠可得，△AOO’是等边三角形，OO’⊥AB，

∵∠ABC＝90°，

∴OO’∥BC，

∴∠ACB＝∠AOO’＝60°，

作P关于AC、BC的对称点G、S，连接GS交AC、BC于M、N，

则此时的周长＝PM+PN+MN=MG+NS+MN＝GS，

∵E、F分别是PG、PS的中点，

∴EF＝GS，

∴当EF取最小值时，GS取最小值，即的周长取最小值，

∵∠PEC＝∠PFC＝90°，

∴C、E、P、F四点共圆且直径为CP，

∵∠ECF＝60°，易得EF＝CP·sin60°＝CP，

故当CP取最小值时，EF取最小值，

连接PC、PO’、CO’，可知，PC+ PO’＞CO’，

∵CO’＝CK+ O’K，且O’K＝PO’，

∴PC＞CK，

故当P、K重合时CP取最小值，此时CP＝CK＝CO’－O’K，

∵AC是直径，

∴AC＝8，∠AO’C＝90°，

∴CO’＝AC·sin60°＝8×＝，

∴CP＝CK＝CO’－O’K＝，

∴EF＝CP＝，

∴GS＝2EF＝，

即周长的最小值为：，

故答案为：.