题目内容
【题目】已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=2![]() .点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
(1)求这条抛物线的解析式;
(2)用含m的代数式表示线段CO的长;
(3)当tan∠ODC=![]() 时,求∠PAD的正弦值.
时,求∠PAD的正弦值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)先根据勾股定理求得![]() 的长度,从而确定
的长度,从而确定![]() 的坐标,代入抛物线解析式即可;(2)可借助三角形相似,
的坐标,代入抛物线解析式即可;(2)可借助三角形相似, ![]() ∽
∽![]() ,利用对应边成比例得到
,利用对应边成比例得到![]() 的表达式;(3)再一次利用三角形相似,
的表达式;(3)再一次利用三角形相似, ![]() ∽
∽![]() ,先求出
,先求出![]() 的表达式,结合
的表达式,结合![]() ,求出
,求出![]() 的值,进而得到
的值,进而得到![]() 坐标以及相关的线段长度,再将
坐标以及相关的线段长度,再将![]() 的正弦值放到
的正弦值放到![]() 中求解即可.
中求解即可.
试卷解析:作图如下:
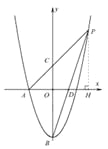
(1)∵![]() ,
, ![]() ,∴
,∴![]() ,即
,即![]() ,∵
,∵![]() 在抛物线上,∴
在抛物线上,∴![]() ,∴
,∴![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)由(1)得![]() (
(![]() ),∴
),∴![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ∽
∽![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() ;
;
(3)∵![]() ,∴
,∴![]() ∽
∽![]() ,∴
,∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴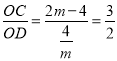 ,解得
,解得![]() 或
或![]() (舍),∴
(舍),∴![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
