题目内容
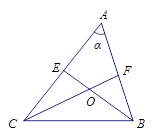
如图，在△ABC中，∠A=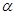
,角平分线BE、CF相交于点O，则∠BOC=( )
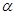,角平分线BE、CF相交于点O，则∠BOC=( )A．90°+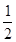 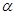| B．90°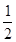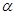－ | C．180°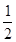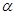＋ | D．180°－ |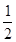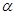
A
本题考查的是三角形的内角和，角平分线的性质
先根据三角形的内角和定理求出∠ABC+∠ACB的度数，再根据角平分线的定义求出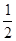
（∠ABC+∠ACB），然后再利用三角形的内角和定理求解即可．
∵∠A=，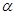
∴∠ABC+∠ACB=180°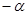
，
∵∠B、∠C的内角平分线交于点O，
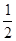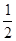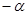∴∠OBC+∠OCB=（∠ABC+∠ACB）=（180°）=90°－，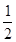
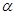在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°－（90°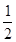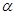－）=180°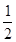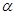－90°+=90°+，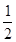
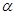故选A.
先根据三角形的内角和定理求出∠ABC+∠ACB的度数，再根据角平分线的定义求出
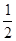（∠ABC+∠ACB），然后再利用三角形的内角和定理求解即可．∵∠A=
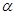，∴∠ABC+∠ACB=180°
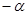，∵∠B、∠C的内角平分线交于点O，
∴∠OBC+∠OCB=
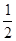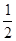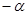（∠ABC+∠ACB）=（180°）=90°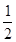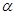－，在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°－（90°－
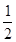
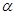）=180°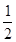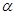－90°+=90°+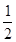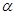，故选A.
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
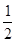∠C.
