题目内容
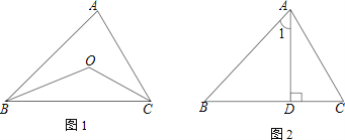
【题目】(1)如图1,△ABC中,∠BAC=60°,内角∠ABC、∠ACB的平分线相交于点O,则∠BOC=______;
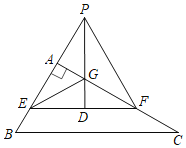
(2)如图2,△ABC中,∠BAC=60°,AD是△ABC的边BC上的高,且∠B=∠1,求∠C的度数.
【答案】(1)120°;(2)∠C=75°
【解析】
(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,由三角形内角和定理即可得出结论;
(2)先求出∠1+∠B的度数,再结合∠1=∠B,求出∠B的度数,最后依据三角形内角和定理求出∠C的度数.
解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∵∠A=60°,
∴∠OBC+∠OCB=![]() (180°-60°)=60°,
(180°-60°)=60°,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-60°
=120°,
故答案为:120°.
(2)∵AD为边BC上的高,
∴∠ADB=90°,
∴∠1+∠B=180°-∠ADB=90°,
又∵∠1=∠B,
∴∠B=![]() ×90°=45°,
×90°=45°,
在△ABC中,∠C=180°-∠B-∠BAC=180°-45°-60°=75°.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
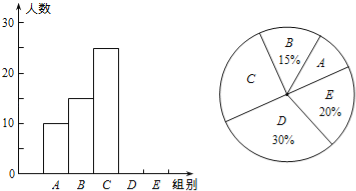
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.