题目内容
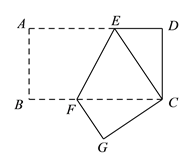
【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
【答案】见解析.
【解析】(1)根据图形折叠前后图形不发生大小变化,证明两角相等推出CE=CF;(2)运用平行四边形的判定和勾股定理列方程求解,再用平行四边形面积公式计算出四边形AFCE的面积.
(1)证明:∵矩形纸片ABCD折叠,顶点A与C重合,折痕为EF,
∴∠1=∠2,AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴CE=CF.
(2)思路:连接AF
① 由矩形纸片ABCD折叠,易证四边形AFCE为平行四边形;
② Rt△CED中,设DE为x,则CE为16-x,CD=8,根据勾股定理列方程可求得DE,CE的长;
③由CF=CE,可得CF的长;
运用平行四边形面积公式计算CF×CD可得四边形AFCE的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目