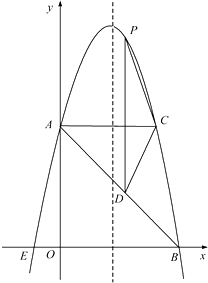
[题目]如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.(1)求证:BD=EC;(2)若AC=2. , 求菱形ABCD的面积. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.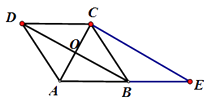

（1）求证:BD=EC;
（2）若AC=2， , 求菱形ABCD的面积.

【答案】
（1）证明：∵四边形ABCD为菱形
∴AB∥CD, AB=CD
∵BE=AB
∴BE∥CD且BE=CD
∴四边形BECD为平行四边形
∴DB=CE
（2）解：∵四边形BECD为平行四边形
∴DB∥CE
∴∠E=∠OBA
∴
∵四边形ABCD为菱形
∴∠AOB=90°,
∴

【解析】（1）要证BD=EC，可证四边形BECD为平行四边形，利用一组对边即BE、CD平行且相等可证出结论;（2）可利用菱形的面积公式，即两对角线积的一半，利用sin ∠ OBA = sin ∠ E，求出OA，进而求出BD,求出面积.

练习册系列答案

相关题目

【题目】如图，在中，对角线交于点，，点分别是的中点，交于点．有下列4个结论：①；②；③；④，其中说法正确的有(　　)

A.1个B.2个C.3个D.4个

【题目】如图，直线与双曲线相交于A（2，1）、B两点．

（1）求m及k的值；

（2）不解关于x、y的方程组直接写出点B的坐标；

（3）直线经过点B吗？请说明理由．

【答案】（1）m=－1，k=2；（2）（－1，－2）；（3）经过

【解析】试题分析：（1）把A（2，1）分别代入直线与双曲线即可求得结果；

（2）根据函数图象的特征写出两个图象的交点坐标即可；

（3）把x=－1，m=－1代入即可求得y的值，从而作出判断.

（1）把A（2，1）分别代入直线与双曲线的解析式得m=－1，k=2；

（2）由题意得B的坐标（－1，－2）；

（3）当x=－1，m=－1代入得y=－2×(－1)+4×(－1)=2－4=－2

所以直线经过点B(－1，－2).

考点：反比例函数的性质

点评：反比例函数的性质是初中数学的重点，是中考常见题，一般难度不大，需熟练掌握.

【题型】解答题
【结束】
20

【题目】某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数，其图象如图所示(千帕是一种压强单位)

（1）写出这个函数的解析式；

（2）当气球的体积为0.8立方米时，气球内的气压是多少千帕；

（3）当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。

【题目】如果反比例函数的图象经过点（3，2），那么下列各点中在此函数图象上的点是（）

A.（-，3）B.（9，）C.（-，2）D.（6，）

【题目】如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c的顶点坐标为(2，9)，与y轴交于点A(0，5)，与x轴交于点E，B.

（1）求二次函数y＝ax2＋bx＋c的解析式；
（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点(点P在AC上方)，作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；
（3）若点M在抛物线上，点N在其对称轴上，使得以A，E，N，M为顶点的四边形是平行四边形，且AE为其一边，求点M，N的坐标．