题目内容
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于(-1,0)点,则下列结论中正确的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
【答案】D
【解析】
由函数图象可知:抛物线开口向下可得出a小于0,与y轴交点在正半轴可得c大于0,与x轴有两个交点可得根的判别式大于0,对称轴在y轴右边,由a小于0,利用左同右异(对称轴在y轴左侧,a与b符号相同;反之符号不同)的判断方法即可得出b的符号,从而得出正确的选项.
因为抛物线开口向下,
所以a<0,
因为抛物线与y轴交点在正半轴,
所以c>0,
由图象可知,当x=-1时,a-b+c=0,
因为抛物线与x轴有两个交点,
所以b2-4ac>0,即b2>4ac,
因为对称轴, ![]()
所以,2a+b=0
故选:D

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
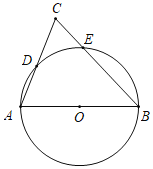
期末集结号系列答案【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.