Question

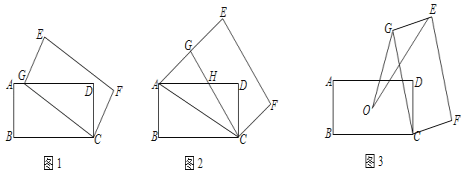
【题目】如图，菱形ABCD中，∠B＝60°，AB＝3cm，过点A作∠EAF＝60°，分别交DC，BC的延长线于点E，F，连接EF．

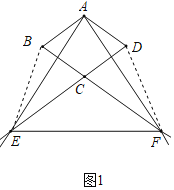
（1）如图1，当CE＝CF时，判断△AEF的形状，并说明理由；

（2）若△AEF是直角三角形，求CE，CF的长度；

（3）当CE，CF的长度发生变化时，△CEF的面积是否会发生变化，请说明理由．

Answer 1

【答案】(1) △AEF是等边三角形，证明见解析；(2) CF＝，CE＝6或CF＝6，CE＝；(3) △CEF的面积不发生变化，理由见解析.

【解析】

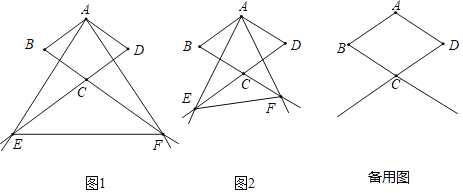
（1）证明△BCE≌△DCF（SAS），得出∠BE＝DF，CBE＝∠CDF，证明△ABE≌△ADF（SAS），得出AE＝AF，即可得出结论；

（2）分两种情况：①∠AFE＝90°时，连接AC、MN，证明△MAC≌△NAD（ASA），得出AM＝AN，CM＝DN，证出△AMN是等边三角形，得出AM＝MN＝AN，设AM＝AN＝MN＝m，DN＝CM＝b，BM＝CN＝a，证明△CFN∽△DAN，得出，得出FN＝，AF＝m+，同理AE＝m+，在Rt△AEF中，由直角三角形的性质得出AE＝2AF，得出m+＝2（m+），得出b＝2a，因此，得出CF＝AD＝，同理CE＝2AB＝6；

②∠AEF＝90°时，同①得出CE＝AD＝，CF＝2AB＝6；

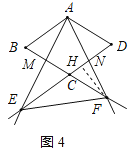
（3）作FH⊥CD于H，如图4所示：由（2）得BM＝CN＝a，CM＝DN＝b，证明△ADN∽△FCN，得出，由平行线得出∠FCH＝∠B＝60°，△CEM∽△BAM，得出，得出，求出CF×CE＝AD×AB＝3×3＝9，由三角函数得出CH＝CF×sin∠FCH＝CF×sin60°＝CF，即可得出结论．

解：（1）△AEF是等边三角形，理由如下：

连接BE、DF，如图1所示：

∵四边形ABCD是菱形，

∴AB＝BC＝DC＝AD，∠ABC＝∠ADC，

在△BCE和△DCF中，，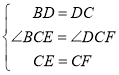

∴△BCE≌△DCF（SAS），

∴∠BE＝DF，CBE＝∠CDF，

∴∠ABC+∠CBE＝∠ADC+∠CDF，

即∠ABE＝∠ADF，

在△ABE和△ADF中，，

∴△ABE≌△ADF（SAS），

∴AE＝AF，又∵∠EAF＝60°，

∴△AEF是等边三角形；

（2）分两种情况：

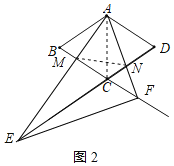
①∠AFE＝90°时，连接AC、MN，如图2所示：

∵四边形ABCD是菱形，

∴AB＝BC＝DC＝AD＝3，∠D＝∠B＝60°，AD∥BC，AB∥CD，

∴△ABC和△ADC是等边三角形，

∴AC＝AD，∠ACM＝∠D＝∠CAD＝60°＝∠EAF，

∴∠MAC＝∠NAD，

在△MAC和△NAD中，，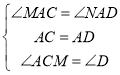

∴△MAC≌△NAD（ASA），

∴AM＝AN，CM＝DN，

∵∠EAF＝60°，

∴△AMN是等边三角形，

∴AM＝MN＝AN，

设AM＝AN＝MN＝m，DN＝CM＝b，BM＝CN＝a，

∵CF∥AD，

∴△CFN∽△DAN，

∴，

∴FN＝，

∴AF＝m+，

同理：AE＝m+，

在Rt△AEF中，∵∠EAF＝60°，

∴∠AEF＝30°，

∴AE＝2AF，

∴m+＝2（m+），

整理得：b2﹣ab﹣2a2＝0，

（b﹣2a）（b+a）＝0，

∵b+a≠0，

∴b﹣2a＝0，

∴b＝2a，

∴＝，

∴CF＝AD＝，

同理：CE＝2AB＝6；

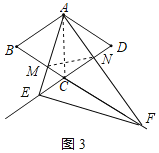
②∠AEF＝90°时，连接AC、MN，如图3所示：

同①得：CE＝AD＝，CF＝2AB＝6；

（3）当CE，CF的长度发生变化时，△CEF的面积不发生变化；理由如下：

作FH⊥CD于H，如图4所示：

由（2）得：BM＝CN＝a，CM＝DN＝b，

∵AD∥CF，

∴△ADN∽△FCN，

∴，

∵CE∥AB，

∴∠FCH＝∠B＝60°，△CEM∽△BAM，

∴，

∴，

∴CF×CE＝AD×AB＝3×3＝9，

∵CH＝CF×sin∠FCH＝CF×sin60°＝CF，

△CEF的面积＝CE×FH＝CE×CF＝×9×＝，∴△CEF的面积是定值，不发生变化．