题目内容
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
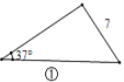

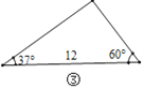
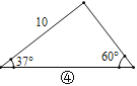
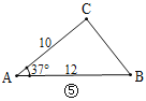
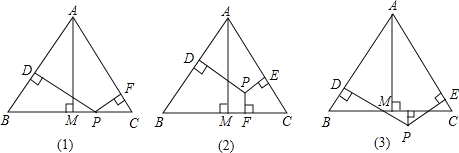
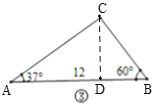
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)③④;(2)能,BC=![]() .
.
【解析】
(1)①只有一个角和一条边不能求出其它元素;②只有三个角,没有已知边,不能求出其它三条边;③知道两个角和一条边,作出相应辅助线,利用三角形内角和定理、锐角三角函数及勾股定理可求出其它元素;④知道两个角和一条边,作出相应辅助线,利用三角形内角和定理、锐角三角函数及勾股定理可求出其它元素;综上即可得答案;
(2)作CD⊥AB于D,利用∠A的正弦和余弦可求出CD和AD的长,进而可求出BD的长,利用勾股定理即可求出BC的长.
(1)①只有一个角和一条边不能求出其它元素;
②只有三个角,没有已知边,不能求出其它三条边;
③如图,作CD⊥AB于D,
∵∠A=37°,∠B=60°,
∴∠ACB=180°-37°-60°=83°,
设AC=x,
∵∠A=37°,CD⊥AB,
∴CD=AC·sin37°=0.6x,AD=0.8x,
∵AB=12,
∴BD=12-x,
∵∠B=60°,
∴tan60°=![]() =
=![]() ,即
,即![]() ,
,
解得:x=![]() ,即AC=
,即AC=![]() .
.
∴BC=![]() =
=![]() =
=![]() .
.
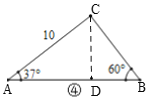
④如图,作CD⊥AB于D,
∵∠A=37°,∠B=60°,
∴∠ACB=180°-37°-60°=83°,
∵∠A=37°,CD⊥AB,AC=10,
∴CD=AC·sin37°=6,AD=AC·cos37°=8,
∵∠B=60°,
∴tan60°=![]() =
=![]() ,
,
∴BD=2![]() ,
,
∴AB=AD+BD=8+2![]() ,BC=
,BC=![]() =4
=4![]() .
.
综上所述:可以求出其余未知元素是③④,
故答案为:③④
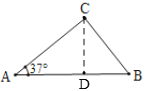
(2)如图,作CD⊥AB于D,
∴∠ADC=90°,
∵AC=10,∠A=37°,
∴CD=AC·sin37°=10×0.6=6,AD=AC·cos37°=10×0.8=8,
∵AB=12,
∴BD=12-8=4,
∴BC=![]() =
=![]() =
=![]() .
.
∴能求出BC的长,BC=![]() .
.

 步步高达标卷系列答案
步步高达标卷系列答案