题目内容
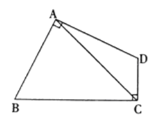
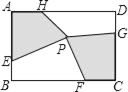
【题目】如图，某塔观光层的最外沿点E为蹦极项目的起跳点．已知点E离塔的中轴线AB的距离OE为10米，塔高AB为123米（AB垂直地面BC），在地面C处测得点E的仰角α=45°，从点C沿CB方向前行40米到达D点，在D处测得塔尖A的仰角β=60°，求点E离地面的高度EF．（结果精确到1米，参考数据 
≈1.4， 
≈1.7）
【答案】解：在直角△ABD中，BD= 
= 
=41 
（米），
则DF=BD﹣OE=41 ﹣10（米），
CF=DF+CD=41 ﹣10+40=41 +30（米），
则在直角△CEF中，EF=CFtanα=41 +30≈41×1.7+30=99.7≈100（米）．
答：点E离地面的高度EF是100米
【解析】在直角△ABD中，利用三角函数求得BD的长，则CF的长即可求得，然后在直角△CEF中，利用三角函数求得EF的长．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
