Question

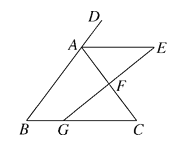
【题目】如图，在等腰△ABC中，AB＝AC，∠A＝20°，AB上一点D，且AD＝BC，过点D作DE∥BC且DE＝AB，连接EC，则∠DCE的度数为（ ）

A. 80° B. 70° C. 60° D. 45°

Answer 1

【答案】B

【解析】

连接AE．根据ASA可证△ADE≌△CBA，根据全等三角形的性质可得AE=AC，∠AED=∠BAC=20°，根据等边三角形的判定可得△ACE是等边三角形，根据等腰三角形的判定可得△DCE是等腰三角形，再根据三角形内角和定理和角的和差关系即可求解．

如图所示，连接AE．

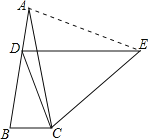
∵AB=DE，AD=BC

∵DE∥BC，

∴∠ADE=∠B，可得AE=DE

∵AB=AC，∠BAC=20°，

∴∠DAE=∠ADE=∠B=∠ACB=80°，

在△ADE与△CBA中，

，

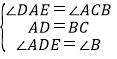∴△ADE≌△CBA（ASA），

∴AE=AC，∠AED=∠BAC=20°，

∵∠CAE=∠DAE-∠BAC=80°-20°=60°，

∴△ACE是等边三角形，

∴CE=AC=AE=DE，∠AEC=∠ACE=60°，

∴△DCE是等腰三角形，

∴∠CDE=∠DCE，

∴∠DEC=∠AEC-∠AED=40°，

∴∠DCE=∠CDE=（180-40°）÷2=70°．

故选B．