题目内容
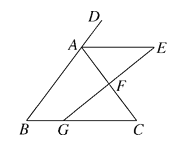
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
【答案】(1)证明见解析;(2)32.
【解析】试题分析:(1)首先依据平行线的性质证明∠B=∠DAE,∠C=∠CAE,然后结合角平分线的定义可证明∠B=∠C,故此可证明△ABC为等腰三角形;
(2)首先证明△AEF≌△CFG,从而得到CG的长,然后可求得BC的长,于是可求得△ABC的周长.
试题解析:证明:(1)∵AE∥BC,∴∠B=∠DAE,∠C=∠CAE.
∵AE平分∠DAC,∴∠DAE=∠CAE,∴∠B=∠C,∴△ABC是等腰三角形.
(2)∵F是AC的中点,∴AF=CF.
在△AFE和△CFG中,∵∠C=∠CAE,AF=FC,∠AFE=∠GFC,∴△AEF≌△CFG,∴AE=GC=8.
∵GC=2BG,∴BG=4,∴BC=12,∴△ABC的周长=AB+AC+BC=10+10+12=32.

练习册系列答案
相关题目
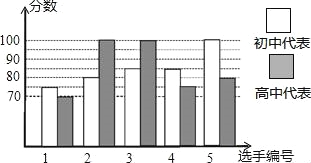
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分 | 中位数/分 | 众数/分 | |
初中代表队 | |||
高中代表队 |
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.