题目内容
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.

⑴说明:OE=OF
⑵当点O运动到何处时,四边形AECF是矩形,证明你的结论
⑶在⑵的条件下,当⊿ABC满足什么条件时,四边形AECF为正方形.
【答案】(1)证明见解析;(2)当点O运动到AC的中点时,证明见解析;(3)△ABC满足∠ACB为直角的直角三角形时,证明见解析.
【解析】
(1)利用平行线的特殊性质,内错角相等,以及角平分线的性质,等量代换,最后求出![]() ;
;
(2)先证明平行四边形,再证明对角线相等,推出四边形为矩形;
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
(1)∵MN∥BC,
∴![]() ,
,![]() ,
,
又已知CE平分∠BCO,CF平分∠DCO,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,![]() ,
,
又∵![]() ,
,
∴四边形AECF是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴四边形AECF是矩形;
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当![]() ,则
,则
![]() ,
,
∴AC⊥EF,
∴四边形AECF是正方形.

 阅读快车系列答案
阅读快车系列答案【题目】如图①,将直角梯形![]() 放在平面直角坐标系中,已知
放在平面直角坐标系中,已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连结
,连结![]() .
.

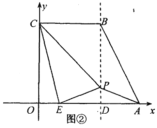
(1)求证:![]() ;
;
(2)如图②,过点![]() 作
作![]() 轴于
轴于![]() ,点
,点![]() 在直线
在直线![]() 上运动,连结
上运动,连结![]() 和
和![]() .
.
①当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标;
的坐标;
②如果点![]() 在
在![]() 轴上方,且满足
轴上方,且满足![]() ,求
,求![]() 的长.
的长.
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.