题目内容
【题目】如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5cm,DF=4cm,那么EF的长为( )
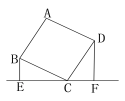
A. 6.5cm B. 6cm C. 5.5cm D. 4cm
【答案】A
【解析】
根据已知条件易证△BCE≌△CDF,再根据全等三角形的性质得到CE=DF,BE=CF,由EF=EC+CF即可求得EF的长.
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD.
又∵BE⊥EF,DF⊥EF,
∴∠BEC=∠CFD=90°,
∵∠CBE+∠ECB=90°,∠DCF+∠ECB=90°,
∴∠CBE=∠DCF,
在△BCE与△CDF中,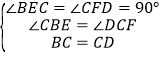 ,
,
∴△BCE≌△CDF(AAS),
∴CE=DF,BE=CF,
又∵BE=2.5cm,DF=4cm,
∴EF=EC+CF=DF+BE=6.5cm.
故选A.

练习册系列答案
相关题目