题目内容
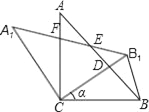
【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长.
【答案】(1)证明见解析;(2)①△BB1D是等腰三角形,理由见解析;②CD=![]() ﹣1.
﹣1.
【解析】
(1)根据已知条件,利用旋转的性质及全等三角形的判定方法,来判定三角形全等.
(2)①根据旋转的性质和等腰三角形的判定与性质得到△BB1D是等腰三角形;
②如图,过D作DG⊥BC于G,设DG=x,通过解直角三角形和已知条件BC=1列出关于x的方程,通过解方程求得x的值,然后易得CD=2x.
(1)∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
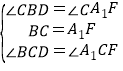
∴△BCD≌△A1CF(ASA).
(2)①△BB1D是等腰三角形,理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1=![]() =75°.
=75°.
∴∠B1BD=∠CBB1﹣∠CBA=75°﹣45°=30°,
∴∠BDB1=480°﹣75°﹣30°=75°,
∴∠BDB1=∠CB1B=∠DB1B=75°,
∴BD=BB1,
∴△BB1D是等腰三角形.
②如图,过D作DG⊥BC于G,设DG=x,
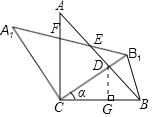
∵ɑ=30°,∠DBE=45°,
∴BG=x,CG=![]() x,
x,
∴![]() x+x=1,
x+x=1,
解得x=![]() ,
,
故CD=2x=![]() ﹣1.
﹣1.

 阅读快车系列答案
阅读快车系列答案