题目内容
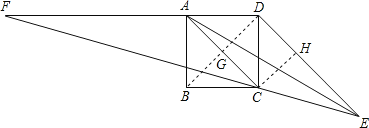
【题目】如图,四边形ABCD为正方形,DE∥AC且CE=CA,直线EC交DA延长线于F.

(1)若CD=6,求DE的长;
(2)求证:AE=AF.
【答案】(1)DE=![]() +
+![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)连接BD,作CH⊥DE于H,根据正方形的性质证明DGCH是正方形,求出2CH=CE,分别在![]() 和
和![]() 中求出DH、EH,即可求出DE的长;
中求出DH、EH,即可求出DE的长;
(2)可证明∠CEH=30°,根据等腰三角形性质和三角形的外角性质求出∠AEC=∠CAE=15°,然后求出∠F的度数即可得证.
解:如图,连接BD,作CH⊥DE于H,
(1)∵ABCD是正方形,
∴∠DGC=90°,GC=DG,
∵AC∥DE,CH⊥DE,
∴∠DHC=∠GCH=∠DGC=90°,
∴四边形CGDH是正方形.
∴CH=DH=![]() CD=
CD=![]() ,
,
∴CE=AC= 2GC=2CH=![]() ,
,
∴EH=![]() ,
,
∴DE=DH+HE=![]() +
+![]() ;
;
(2)由(1)可知CE=2CH,
∴∠CEH=30°,
又CE=AC,
∴∠CAE=∠CEA=∠AED=15°,
又∵∠FAE=90°+45°+15°=150°,
∴∠F=180°-150°-15°=15°,
∴∠F=∠AEF,
∴AE=AF.

练习册系列答案
相关题目