��Ŀ����
����Ŀ����ͼ1����ABC�У�CD��AB��D����BD=4��AD=6��CD=8��
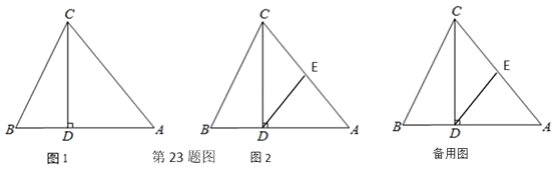
��1����֤����ACB=��ABC��
��2����ͼ2��EΪAC���е㣬����DE������M�ӵ�B������ÿ��1cm���ٶ����߶�BA���A �˶���ͬʱ����N�ӵ�A��������ͬ�ٶ����߶�AC���C�˶���������һ�㵽���յ�ʱ��һ����Ҳֹͣ�˶������M�˶���ʱ��Ϊt���룩��
����MN��BCƽ�У���t��ֵ��
�����ڵ�M�˶��Ĺ����У���MDE�ܷ��Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
���𰸡���1������������2����t=5����tֵΪ9��10�� ![]()
��������
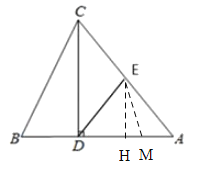
��1�������AB�ij��������ù��ɶ������AC�ij�����AB=AC���ȱ߶ԵȽǼ��ɵó���ACB=��ABC����2���� ������֪AB=AC����˵�AM=ANʱ�� MN��BC �����ǽ��·�̵Ĺ�ϵ�з��̣����t���ɣ�����ΪBD<DE����M��BD��ʱ����BDE�����ܹ��ɵ��������Σ���M��DA��ʱ������������ֱ���⣬��DE=DM����t-4=5�����t���ɣ������ED=EM����M�պ��˶�����A�� ��Ȼt=10�� ���MD=ME����E��EH��AD����EH��HM�ֱ��ú�t�Ĵ���ʽ��ʾ���ڡ�EHM�У������ù��ɶ�����ʽ���t���ɣ�
�⣺
��1��֤������AB=AD+BD=6+4=10��
AC=![]() ��
��
��AB=AC��
�� ��ACB=��ABC.
��2���⣺��ͼ��
���������BM=t��AN=t����AM=10-t��
��MN��BCʱ��AM=AN��
��10��t=t��
��t=5��
�ڵ���M��DA�ϣ���4��t��10ʱ����MDEΪ���������Σ���3�ֿ��ܣ�
��CD��AB��
���CDA=90�㣬
��EΪAC�е㣬
��DE=![]() AC=5��
AC=5��
���DE=DM����t��4=5��
��t=9��
���ED=EM�����M�˶�����A��
��t=10��
���MD=ME=t��4����E��EH��AD��
��EH��AD��CD��AD��
��EH��CD��
��EΪAC�е㣬
��AE=![]() CD=4��
CD=4��
��![]() ��
�У�
DH=![]() ��
��
��HM=DM-DH=t-4-3=t-7��
����EHM��
��t��4��2����t��7��2=42��
��t= ![]() ��
��
��������������Ҫ���tֵΪ9��10�� ![]() ��
��

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�