题目内容
【题目】如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠BAC,DE⊥AB于E,有下列结论：①DE=DC；②∠BDE=∠ADC；③AB=2AC；④图中共有两对全等三角形.其中正确的是：____________（填序号即可）.
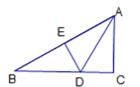
【答案】①②③
【解析】
根据题意可证△AED≌△ACD即可判断①；再证△BED≌△AED即可判断②③，最后证△BED≌△ACD即可判断④.
∵AD平分∠BAC，∠B=30°，∠C=90°
∴∠EAD=∠CAD=30°
又DE⊥AB于E
∴∠DEA=∠BED=90°
在△AED和△ACD中
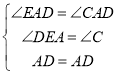
∴△AED≌△ACD（AAS）
∴DE=DC，∠EDA=∠CDA，AC=AE故①正确
在△BED和△AED中
∴△BED≌△AED（AAS）
∴∠BDE=∠ADE，BE=AE
∴∠BDE=∠CDA，故②正确
又BE+AE=AB
∴AB=2AE=2AC，故③正确
在△BED和△ACD中
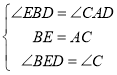
∴△BED≌△ACD（SAS），共有3对全等三角形，故④错误
故答案为：①②③.
练习册系列答案
相关题目
【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表
组别 | 分组（单位：元） | 人数 |
A | 0≤x＜30 | 4 |
B | 30≤x＜60 | 16 |
C | 60≤x＜90 | a |
D | 90≤x＜120 | b |
E | x≥120 | 2 |
请根据以上图表，解答下列问题：
（1）填空：这次被调查的同学共有__人，a+b=__，m=___；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在60≤x＜120范围的人数．
