题目内容
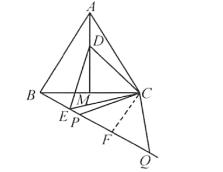
【题目】如图,在等边△ABC中, M为BC边上的中点, D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE.
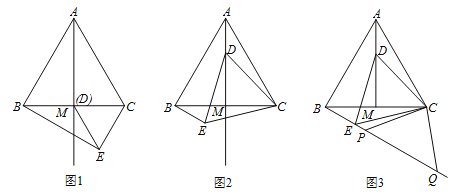
(1)填空:若D与M重合时(如图1)∠CBE= 度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(2)的条件下,如图3,若点P、Q在BE的延长线上,且CP=CQ=4,AB=6,试求PQ的长.
【答案】(1)30°(2)(1)中结论成立.理由见解析(3)![]() .
.
【解析】
(1)如图1.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,
∵△CDE是等边三角形,
∴∠CDE=60°,CD=DE,
∴BD=DE,
∴∠BED=∠DBE,
又∵∠BED+∠DBE=∠CDE=60°,
∴∠DBE=30°,即∠CBE=30°;
故答案为30;
(2)(1)中结论成立.
证明:∵正△ABC、正△CDE ∴AC=BC,EC=DC,∠ACB=∠DCE=60°, ∴∠ACD=∠BCE
∴△ACD≌△BCE ∴∠CAD=∠CBE. 又∵正△ABC中,M是BC中点.
∴∠CAD=![]() ∠BAC=30°. ∴∠CBE=30°
∠BAC=30°. ∴∠CBE=30°
(3)
作CF⊥PQ于F ∵CP=CQ ∴PF=QF=![]() PQ
PQ
由(2)Rt△BCF中,∠CBF=30° ∴CF=![]() BC=
BC=![]() AB=3
AB=3
Rt△PCF中,PF=![]() ∴PQ=2PF=
∴PQ=2PF=![]()

 阅读快车系列答案
阅读快车系列答案【题目】某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
(1)设答对一题记a分,答错一题记b分,则a= b= ;
(2)参赛者E说他得了80分,你认为可能吗,为什么?
【题目】已知![]() 两点在数轴上从各自位置同时向左右匀速运动(规定向右为正)
两点在数轴上从各自位置同时向左右匀速运动(规定向右为正)
时间 位置 | 0秒 | 3秒 | 6秒 |
| 6 | -3 | |
| 2 | 8 |
(1)请你将上面表格补充完整;
(2)点![]() 、点
、点![]() 运动过程中是否会相遇,如果能相遇,请求出相遇的时间
运动过程中是否会相遇,如果能相遇,请求出相遇的时间
(3)点![]() 、点
、点![]() 两点间的距离能否为5个单位长度?若能,请求出它们运动的时间
两点间的距离能否为5个单位长度?若能,请求出它们运动的时间