题目内容
【题目】如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.
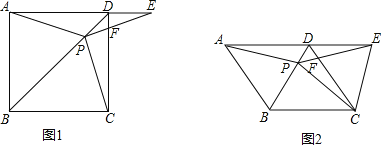
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
【答案】(1)见解析;(2)△PCE是等边三角形.理由见解析.
【解析】
(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=EDF=90°,推出△PEC是等腰直角三角形;
(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA═PE=PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.
(1)证明:如图1中,
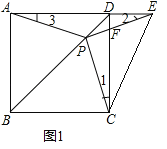
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,
在△PDA和△PDC中,
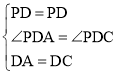 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,
∴∠1=∠2,
∵∠EDF=90°,∠DFE=∠PFC,
∴∠FPC=EDF=90°,
∴△PEC是等腰直角三角形.
(2)解:如图2中,结论:△PCE是等边三角形.
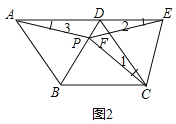
理由:∵四边形ABCD是菱形,
∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,
在△PDA和△PDC中,
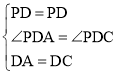 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,PA═PE=PC,
∴∠1=∠2,
∵∠DFE=∠PFC,
∴∠EPC=∠EDC,
∵∠ADC=120°,
∴∠EDC=60°,
∴∠EPC=60°,
∵PE=PC,
∴△PEC是等边三角形.

【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?
【题目】某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
(1)设答对一题记a分,答错一题记b分,则a= b= ;
(2)参赛者E说他得了80分,你认为可能吗,为什么?