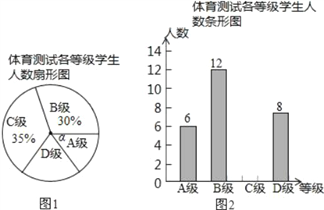
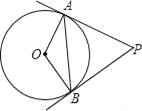
题目内容
【题目】一个正方体物体沿斜坡向下滑动，其截面如图所示．正方形DEFH的边长为2米，坡角∠A=30°，∠B=90°，BC=6米．当正方形DEFH运动到什么位置，即当AE=
米时，有DC2=AE2+BC2．
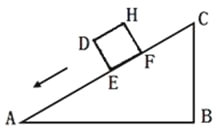
【答案】：解：假设AE=x，可得EC=12﹣x，
∵坡角∠A=30°，∠B=90°，BC=6米，
∴AC=12米，
∵正方形DEFH的边长为2米，即DE=2米，
∴DC2=DE2+EC2=4+（12﹣x）2，
AE2+BC2=x2+36，
∵DC2=AE2+BC2，
∴4+（12﹣x）2=x2+36，
解得：x=
米．
故答案为：．
【解析】：根据已知得出假设AE=x，可得EC=12﹣x，利用勾股定理得出DC2=DE2+EC2=4+（12﹣x）2，AE2+BC2=x2+36，即可求出x的值．
【题目】某书定价8元，如果一次购买10本以上，超过10本部分打八折，那么付款金额y与购书数量x之间的函数关系如何，同学们对此展开了讨论： ⑴小明说：y与x之间的函数关系为y=6.4x+16
⑵小刚说：y与x之间的函数关系为y=8x
⑶小聪说：y与x之间的函数关系在0≤x≤10时，y=8x；在x＞10时，y=6.4x+16
⑷小斌说：我认为用下面的列表法也能表示它们之间的关系
购买量/本 | 1 | 2 | 3 | 4 | … | 9 | 10 | 11 | 12 | … |
付款金额/元 | 8 | 16 | 24 | 32 | … | 72 | 80 | 86.4 | 92.8 | … |
⑸小志补充说：如图所示的图象也能表示它们之间的关系．
其中，表示函数关系正确的个数有（ ）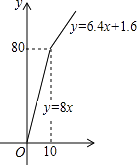
A.1个
B.2个
C.3个
D.4个
【题目】下表是七年级三班30名学生期末考试数学成绩表（已破损）
成绩（分） | 50 | 60 | 70 | 80 | 90 | 100 |
人数（人） | 2 | 5 | 7 | 3 |
已知该班学生期末考试数学成绩平均分是76分．
（1）求该班80分和90分的人数分别是多少？
（2）设该班30名学生成绩的众数为a，中位数为b，求a+b的值．
