题目内容
【题目】已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.

(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
【答案】(1)y=![]() x2-1.
x2-1.
(2)直线l与⊙A相切
(3)![]()
【解析】(1)因为当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,故b=0.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=ax2+bx+c,得
![]() 解得
解得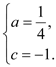
∴这条抛物线的解析式为y=![]() x2-1.
x2-1.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=kx+b,得
![]() 解得
解得
∴这条直线的解析式为y=-![]() x+1.
x+1.
(2)依题意,OA=![]() 即⊙A的半径为5.
即⊙A的半径为5.
而圆心到直线l的距离为3+2=5.
即圆心到直线l的距离=⊙A的半径,
∴直线l与⊙A相切.
(3)由题意,把x=-1代入y=-![]() x+1,得y=
x+1,得y=![]() ,即D(-1,
,即D(-1, ![]() ).
).
由(2)中点A到原点距离跟到直线y=-2的距离相等,且当点A成为抛物线上一个动点时,仍然具有这样的性质,于是过点D作DH⊥直线l于H,交抛物线于点P,此时易得DH是D点到l最短距离,点P坐标(-1,-![]() )此时四边形PDOC为梯形,面积为
)此时四边形PDOC为梯形,面积为![]() .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目