��Ŀ����
ij��Ʒˮ����������һ�ֽ���ˮ��A����ȥ��1��7�£�����ˮ���Ľ���һ·������ÿǧ��A�Ľ��� ���·�
���·� ��
�� ����
���� Ϊ��������֮��ĺ�����ϵʽ���±� ��
Ϊ��������֮��ĺ�����ϵʽ���±� ��
�����ҹ���һЩ���ҽ����ڹ�˰�ĵ�������ˮ���Ľ���������������8��12�·�ÿǧ��ˮ��A�Ľ��� ���·�
���·� ��
�� ����
���� Ϊ������֮���������ͼ��ʾ�ı仯����.
Ϊ������֮���������ͼ��ʾ�ı仯����.
��1����۲�����ͼ������ѧ����һ�κ��������������������κ������й�֪ʶ�ֱ�д�� ��
�� ��
�� ��
�� �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
��2����ȥ���ˮ�����ۼ�Ϊÿǧ��180Ԫ�������۸�ˮ��ÿ�±���֧�����������⣩�Ĺ̶�֧��Ϊ300Ԫ����֪��ˮ����1����7�µ�����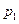 ��ǧ�ˣ����·�
��ǧ�ˣ����·� ���㣺
���㣺 ��8����12�µ�����
��8����12�µ����� ��ǧ�ˣ����·�
��ǧ�ˣ����·� ���㣺
���㣺 �����ˮ���ڵڼ�������ʱ����ʹ��������õ�������������ʱ���������.
�����ˮ���ڵڼ�������ʱ����ʹ��������õ�������������ʱ���������.
��3������1�µ�6�£��ý���ˮ���Ľ��۽��е�����ÿ�½��۾���ȥ��12�µĽ�������15Ԫ����ÿ�µĹ̶�֧�����������⣩������15%����֪�ý���ˮ�����ۼ���ȥ��Ļ���������� ��
�� <100�������ͬʱÿ�µ���������ȥ��12�µĻ����ϼ�����
<100�������ͬʱÿ�µ���������ȥ��12�µĻ����ϼ����� ������������ȥҪʹ����1��6�µ�������Ϊ68130Ԫ�������
������������ȥҪʹ����1��6�µ�������Ϊ68130Ԫ������� ��ֵ.������������Ч���֣����ο����ݣ�
��ֵ.������������Ч���֣����ο����ݣ�
 ��
�� ��
�� ��
��
 ���·�
���·� ��
�� ����
���� Ϊ��������֮��ĺ�����ϵʽ���±� ��
Ϊ��������֮��ĺ�����ϵʽ���±� ���·� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 ��Ԫ/ǧ�ˣ� ��Ԫ/ǧ�ˣ� | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
 ���·�
���·� ��
�� ����
���� Ϊ������֮���������ͼ��ʾ�ı仯����.
Ϊ������֮���������ͼ��ʾ�ı仯����.��1����۲�����ͼ������ѧ����һ�κ��������������������κ������й�֪ʶ�ֱ�д��
 ��
�� ��
�� ��
�� �ĺ�����ϵʽ.
�ĺ�����ϵʽ.��2����ȥ���ˮ�����ۼ�Ϊÿǧ��180Ԫ�������۸�ˮ��ÿ�±���֧�����������⣩�Ĺ̶�֧��Ϊ300Ԫ����֪��ˮ����1����7�µ�����
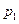 ��ǧ�ˣ����·�
��ǧ�ˣ����·� ���㣺
���㣺 ��8����12�µ�����
��8����12�µ����� ��ǧ�ˣ����·�
��ǧ�ˣ����·� ���㣺
���㣺 �����ˮ���ڵڼ�������ʱ����ʹ��������õ�������������ʱ���������.
�����ˮ���ڵڼ�������ʱ����ʹ��������õ�������������ʱ���������.��3������1�µ�6�£��ý���ˮ���Ľ��۽��е�����ÿ�½��۾���ȥ��12�µĽ�������15Ԫ����ÿ�µĹ̶�֧�����������⣩������15%����֪�ý���ˮ�����ۼ���ȥ��Ļ����������
 ��
�� <100�������ͬʱÿ�µ���������ȥ��12�µĻ����ϼ�����
<100�������ͬʱÿ�µ���������ȥ��12�µĻ����ϼ����� ������������ȥҪʹ����1��6�µ�������Ϊ68130Ԫ�������
������������ȥҪʹ����1��6�µ�������Ϊ68130Ԫ������� ��ֵ.������������Ч���֣����ο����ݣ�
��ֵ.������������Ч���֣����ο����ݣ�
 ��
�� ��
�� ��
��
�ɱ����֪�� ��
�� ��һ�κ�����
��һ�κ�����
�� ��0����
��0����
����1��50������2��60���ֱ�����
 ������������
������������ 
�� =10
=10 +40����������������������������������������������������������1��
+40����������������������������������������������������������1��
����֤�������ֵҲ������˺�����ϵʽ��
�� =10
=10 +40����������������������������������������������������������2��
+40����������������������������������������������������������2��
�� ��0����
��0����
�����꣨8��15����12��135���ֱ�����

�� =5
=5 +75����������������������������������������������������������3��
+75����������������������������������������������������������3��
�裺����ΪWԪ��
��1�� ��7ʱ��
��7ʱ��
W1

 ��
��
�൱ =3ʱ��W1�����ֵ��
=3ʱ��W1�����ֵ�� ��11800 ����������������������������������5��
��11800 ����������������������������������5��
��8�� ��12ʱ��
��12ʱ��
W2
=(-5 +105)(-10
+105)(-10 +250)-300
+250)-300
=50 2-2300
2-2300 +25950��
+25950��
��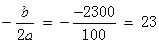 ����
���� ��
��
��W2�� �����������
�������С���� =8ʱ��W2�����ֵ��
=8ʱ��W2�����ֵ��
W2��=10750��
��W1��>W2��
���ڵ�3��ʱ���ɻ��������11800����������������������������������������7��
��3��
 ��68130 ������������������������������������������������������������������8��
��68130 ������������������������������������������������������������������8��
�� %=
%= ��ԭ���̻�Ϊ
��ԭ���̻�Ϊ  ��
��
������ ����
���� ��
��
 ��
��
�� ��33��
��33��  =450(��)��
=450(��)��
�� =33��
=33��
���� ��ֵΪ33������������������������������������������������������10��
��ֵΪ33������������������������������������������������������10��
 ��
�� ��һ�κ�����
��һ�κ�������
 ��0����
��0��������1��50������2��60���ֱ�����
 ������������
������������ 
��
 =10
=10 +40����������������������������������������������������������1��
+40����������������������������������������������������������1������֤�������ֵҲ������˺�����ϵʽ��
��
 =10
=10 +40����������������������������������������������������������2��
+40����������������������������������������������������������2����
 ��0����
��0���������꣨8��15����12��135���ֱ�����

��
 =5
=5 +75����������������������������������������������������������3��
+75����������������������������������������������������������3���裺����ΪWԪ��
��1��
 ��7ʱ��
��7ʱ��W1


 ��
���൱
 =3ʱ��W1�����ֵ��
=3ʱ��W1�����ֵ�� ��11800 ����������������������������������5��
��11800 ����������������������������������5����8��
 ��12ʱ��
��12ʱ��W2

=(-5
 +105)(-10
+105)(-10 +250)-300
+250)-300=50
 2-2300
2-2300 +25950��
+25950����
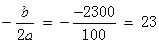 ����
���� ��
����W2��
 �����������
�������С���� =8ʱ��W2�����ֵ��
=8ʱ��W2�����ֵ��W2��=10750��
��W1��>W2��
���ڵ�3��ʱ���ɻ��������11800����������������������������������������7��
��3��
 ��68130 ������������������������������������������������������������������8��
��68130 ������������������������������������������������������������������8����
 %=
%= ��ԭ���̻�Ϊ
��ԭ���̻�Ϊ  ��
��������
 ����
���� ��
�� ��
����
 ��33��
��33��  =450(��)��
=450(��)����
 =33��
=33������
 ��ֵΪ33������������������������������������������������������10��
��ֵΪ33������������������������������������������������������10����

��ϰ��ϵ�д�
�����Ŀ
 ����A(0,2)��B(3,0)����,��ô���һ�κ�����ϵʽ��( )
����A(0,2)��B(3,0)����,��ô���һ�κ�����ϵʽ��( )



 ��һ�κ�������m= ��n .
��һ�κ�������m= ��n .
 ��ͼ������ǣ� ��
��ͼ������ǣ� ��
 �ĺ�����ϵʽ��
�ĺ�����ϵʽ��