题目内容
如图①,在Rt△ABC中,∠C=90°,边BC的长为20cm,边AC的长为hcm,在此三角形内有一个矩形CFED,点D,E,F分别在AC,AB,BC上,设AD的长为xcm,矩形CFED的面积为y(单位:cm2).(1)当h等于30时,求y与x的函数关系式;(不要求写出自变量x的取值范围)
(2)在(1)的条件下,矩形CFED的面积能否为180cm2?请说明理由;
(3)若y与x的函数图象如图②所示,求此时h的值.
(参考公式:二次函数y=ax2+bx+c,当x=-
| b |
| 2a |
| 4ac-b2 |
| 4a |
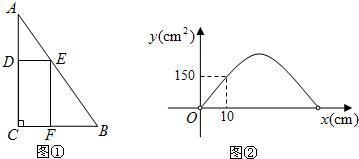
分析:(1)根据AC的长,可用AD表示出CD,根据∠A的正切值,可用AD表示出DE,由此可得出关于y,x的函数关系式.
(2)将y=180代入(1)的函数式中,如果得出的方程有解,就说明矩形的面积能够成为180cm2,反之则不能.
(3)根据(1)的解题思路不难得出含h的关于x,y的函数关系式,然后将图象中的(10,150)的坐标代入抛物线的解析式中,即可求出h的值.
(2)将y=180代入(1)的函数式中,如果得出的方程有解,就说明矩形的面积能够成为180cm2,反之则不能.
(3)根据(1)的解题思路不难得出含h的关于x,y的函数关系式,然后将图象中的(10,150)的坐标代入抛物线的解析式中,即可求出h的值.
解答:解:(1)∵AC=30,AD=x,
∴CD=30-x.
∵四边形CFED为矩形,
∴DE∥BC.
∴
=
,即
=
.
∴DE=
x.
∴y=
x(30-x).
即y=-
x2+20x.
(2)∵
=
=150,
∴y的最大值为150.
∵150<180,
∴矩形CFED的面积不能为180cm2.
(3)由图象可知,当x=10时,y=150.
当x=10时,CD=h-10,DE=
,
∴
(h-10)=150,
解得h=40.
经检验h=40是方程的解.
∴h=40.
∴CD=30-x.
∵四边形CFED为矩形,
∴DE∥BC.
∴
| DE |
| BC |
| AD |
| AC |
| DE |
| 20 |
| x |
| 30 |
∴DE=
| 2 |
| 3 |
∴y=
| 2 |
| 3 |
即y=-
| 2 |
| 3 |
(2)∵
| 4ac-b2 |
| 4a |
4×(-
| ||
4×(-
|
∴y的最大值为150.
∵150<180,
∴矩形CFED的面积不能为180cm2.
(3)由图象可知,当x=10时,y=150.
当x=10时,CD=h-10,DE=
| 200 |
| h |
∴
| 200 |
| h |
解得h=40.
经检验h=40是方程的解.
∴h=40.
点评:本题结合了直角三角形与矩形的相关知识考查了二次函数的应用,综合性较强,难度适中.

练习册系列答案
相关题目