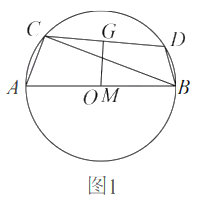题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() 点,若
点,若![]() ,则
,则![]() 的半径为( )
的半径为( )
A.![]() B.5C.
B.5C.![]() D.
D.![]()
【答案】C
【解析】
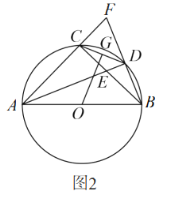
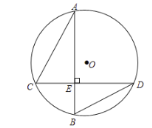
由AB⊥CD,∠CDB=30°,在Rt△BDE中可以先求出EB;由同弧所对圆周角相等,则∠CAE=30°,在Rt△ACE中由AC可以求出CE;连接BC,由勾股定理可求出BC;连接OC,OB可知∠COB=2∠CDB=60°,此时△COB为等边三角形,半径长即为CB的长.
解:如下图所示:连接OC、OB、CB,
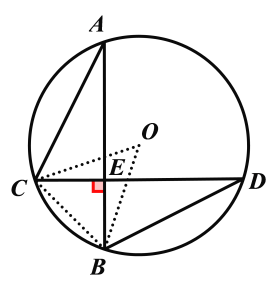
∵AB⊥CD,∠CDB=30°,BD=4,
∴BE=![]() BD=2,
BD=2,
由同弧所对圆周角相等知:∠CAB=∠CDB=30°,
由AC=6,可知CE=3,
在Rt△CEB中,由勾股定理可知:![]()
由同弧所对圆周角等于圆心角的一半知:
∠COB=2∠CDB=60°,且OC=OB,
此时△COB为等边三角形,
∴半径即为![]() .
.
故答案为:C.

【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位计划组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览著名景点“大唐芙蓉园”,该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 108 | 96 |
(1)求团体票价![]() 与游览人数
与游览人数![]() 之间的函数关系式;
之间的函数关系式;
(2)若该单位购买团体票共花费3456元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
【题目】某数学兴趣小组的同学在研究函数![]() 的图象时,先对函数
的图象时,先对函数![]() 的图象进行了如下探索.
的图象进行了如下探索.
![]() ①列表:列出
①列表:列出![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描点:根据表中数据描点如图所示;
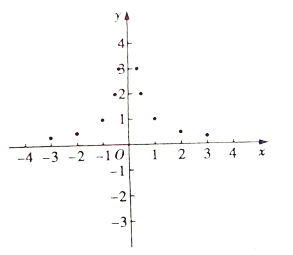
③连线:请在图中画出函数![]() 的图象;
的图象;
④观察图象,写出两条关于该函数的性质.
![]() 根据以上探究结果,完成下列问题:
根据以上探究结果,完成下列问题:
①函数![]() 中,自变量
中,自变量![]() 的取值范围为 ;
的取值范围为 ;
②函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
③写出两条关于函数![]() 的性质;
的性质;
④直接写出不等式![]() 的解集.
的解集.