题目内容
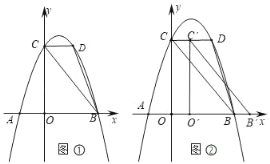
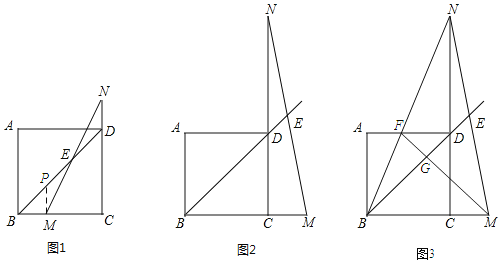
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN,直线BD与MN交于点E.
(1)如图1.当点M在BC上时,为证明“BD﹣2DE=![]() BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.
BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.
(2)如图2,当点M在BC的延长线上时,则BD,DE,BM之间满足的数量关系是 .
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G,如图3,若![]() CM=2,则线段DG= .
CM=2,则线段DG= .
【答案】(1)见解析;(2)BD+2DE=![]() BM;(3)
BM;(3)![]() .
.
【解析】
(1)过点M作MP∥CD,交BD于点P,推出PM=DN,证明△EPM≌△EDN,推出EP=ED,根据正方形的性质和勾股定理求出即可;
(2)过点M作MP∥CD交BD的延长线于点P,推出BM=PM=DN,根据AAS证明△EPM≌△EDN,推出EP=ED,根据正方形的性质和勾股定理求出即可;
(3)证明△ABF∽△DNF,得出比例式,得到AB:ND=1:2,设AB=x,则DN=2x,
根据BM=DN,列出方程求出AB的长度,根据DF∥BM,得到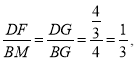 即可求解.
即可求解.
解:(1)如图1,过点M作MP∥CD,交BD于点P,
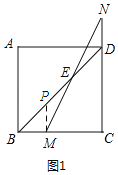
∵四边形ABCD是正方形,
∴∠C=90°,∠CBD=∠CDB=45°,
∵PM∥CD,
∴∠NDE=∠MPE,∠BPM=∠CDB=45°,
∴△BPM是等腰直角三角形,
∴PM=BM,![]()
∵BM=DN,
∴PM=DN,
在△EPM和△EDN中,
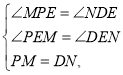
∴△EPM≌△EDN(AAS),
∴EP=ED,
∴PB=BD﹣PD=BD﹣2DE,
根据勾股定理得:![]()
即![]()
(2)如图2,过点M作MP∥CD交BD的延长线于点P,

∴∠PMB=∠BCD=90°,
∵∠CBD=45°,
∴△BMP是等腰直角三角形,
∴BM=PM=DN,
与(1)证法类似:△EPM≌△EDN(AAS),
∴EP=ED,
∴PB=BD+PD=BD+2DE,
根据勾股定理得:BP=![]() BM,
BM,
即BD+2DE=BP=![]() BM,
BM,
故答案为:BD+2DE=![]() BM;
BM;
(3)如图3,∵
∴AB∥DN,

∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
设AB=x,则DN=2x,
∵BM=DN,
∴x+2=2x,x=2,
∴AB=AD=2,DF=![]() ,
,
∴![]()
∵DF∥BM,
∴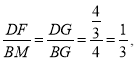
∴![]()
故答案为:![]()

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案