ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ°≈ΉΈοœΏyΘΫax2+bx+3Θ®aΓΌ0Θ©”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎAΘ®©¹1Θ§0Θ©ΓΔBΘ®3Θ§0Θ©ΓΔC»ΐΒψΘ°
Θ®1Θ©«σaΚΆbΒΡ÷ΒΘΜ
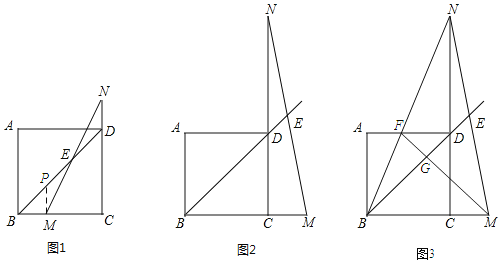
Θ®2Θ©ΒψDΘ®2Θ§mΘ©‘ΎΒΎ“ΜœσœόΒΡ≈ΉΈοœΏ…œΘ§Ν§Ϋ”BCΓΔBDΓΔCDΘ§‘ΎΕ‘≥Τ÷αΉσ≤ύΒΡ≈ΉΈοœΏ…œ¥φ‘Ύ“ΜΒψPΘ§¬ζΉψΓœPBCΘΫΓœDBCΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ
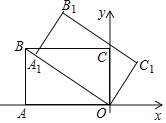
Θ®3Θ©»γΆΦΔΎΘ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬ΫΪΓςBOC―Ίx÷α’ΐΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ”“ΤΫ“ΤΘ§Φ«ΤΫ“ΤΚσΒΡ»ΐΫ«–ΈΈΣΓςB'O'C'‘ΎΤΫ“ΤΙΐ≥Χ÷–Θ§ΓςB'O'C'”κΓςBCD÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΦ«ΈΣSΘ§…ηΤΫ“ΤΒΡ ±Έ ΈΣtΟκΘ§«κ÷±Ϋ”–¥≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ®≤ΔΉΔΟςΉ‘±δΝΩΒΡ»Γ÷ΒΖΕΈßΘ©Θ°
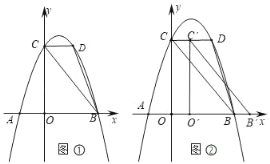
ΓΨ¥πΑΗΓΩΘ®1Θ©aΘΫ©¹1Θ§bΘΫ2ΘΜΘ®2Θ©¥φ‘ΎΘ§PΘ®©¹![]() Θ§
Θ§![]() Θ©ΘΜΘ®3Θ©
Θ©ΘΜΘ®3Θ©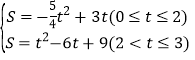 Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫΪΒψAΓΔB¥ζ»κΫβΈω ΫΦ¥Ω…«σ≥ωaΓΔbΒΡ÷ΒΘ°
Θ®2Θ©ΗυΨί“―÷ΣΧθΦΰ«σ≥ωΒψDΒΡΉχ±ξΘ§≤Δ«“”…œΏΕΈOCΓΔOBœύΒ»ΓΔCDΓΈx÷αΦΑΒ»―ϋ»ΐΫ«–Έ–‘÷ ÷ΛΟςΓςCDBΓ’ΓςCGBΘ§άϊ”Ο»ΪΒ»»ΐΫ«–Έ«σ≥ωΒψGΒΡΉχ±ξΘ§«σ≥ω÷±œΏBPΒΡΫβΈω ΫΘ§ΝΣΝΔΕΰ¥ΈΚ· ΐΫβΈω ΫΘ§«σ≥ωΒψPΒΡΉχ±ξΘ°
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘ§ΒΎ“Μ÷÷«ιΩω÷ΊΒΰΟφΜΐΈΣΥΡ±Ώ–ΈΘ§άϊ”Ο¥σ»ΐΫ«–ΈΦθ»ΞΝΫΗω–Γ»ΐΫ«–Έ«σΒΟΫβΈω ΫΘ§ΒΎΕΰ÷÷«ιΩω÷ΊΒΰ≤ΩΖ÷ΈΣ»ΐΫ«–ΈΘ§Ω…άϊ”Ο»ΐΫ«–ΈΒΡΟφΜΐΙΪ Ϋ«σΒΟΘ°
Θ®1Θ©ΫΪΒψAΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©¥ζ»κ≈ΉΈοœΏΘ§
![]() Θ§
Θ§
ΫβΒΟaΘΫ©¹1Θ§bΘΫ2Θ°
Θ®2Θ©¥φ‘ΎΘ§
ΫΪΒψD¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚmΘΫ3Θ§
ΓύDΘ®2Θ§3Θ©Θ§
ΝνxΘΫ0Θ§yΘΫ3Θ§
ΓύCΘ®0Θ§3Θ©Θ§
ΓύOCΘΫOBΘ§
ΓύΓœOCBΘΫΓœCBOΘΫ45ΓψΘ§
»γΆΦ1Υυ ΨΘ§
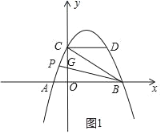
ΓΏCDΓΈx÷αΘ§
ΓύΓœDCBΘΫΓœBCOΘΫ45ΓψΘ§
‘ΎΓςCDBΚΆΓςCGB÷–Θ§
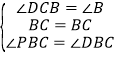
ΓύΓςCDBΓ’ΓςCGBΘ®ASAΘ©Θ§
ΓύCGΘΫGDΘΫ2Θ§
ΓύOGΘΫ1Θ§
ΓύGΘ®0Θ§1Θ©Θ§
…η÷±œΏBPΘΚyΘΫkx+1Θ§
¥ζ»κΒψBΘ§
ΓύkΘΫ©¹![]() Θ§
Θ§
Γύ÷±œΏBPΘΚyΘΫ©¹![]() x+1Θ§
x+1Θ§
ΝΣΝΔ÷±œΏBPΚΆΕΰ¥ΈΚ· ΐΫβΈω ΫΘ§
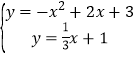
ΫβΒΟ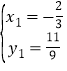 Μρ
Μρ![]() Θ®…αΘ©Θ§
Θ®…αΘ©Θ§
ΓύP![]() Θ°
Θ°
Θ®3Θ©÷±œΏBCΘΚyΘΫ©¹x+3Θ§÷±œΏBDΘΚyΘΫ©¹3x+9Θ§
Β±0ΓήtΓή2 ±Θ§»γΆΦ2Υυ ΨΘ§
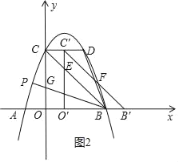
…η÷±œΏBΓδCΓδΘΚyΘΫ©¹Θ®x©¹tΘ©+3Θ§
ΝΣΝΔ÷±œΏBD«σΒΟFΘ®![]() Θ©Θ§
Θ©Θ§
SΘΫ![]() Θ°
Θ°
Β±2ΘΦtΓή3 ±Θ§»γΆΦ3Υυ ΨΘ§
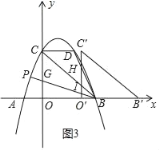
HΘ®tΘ§©¹3t+9Θ©Θ§IΘ®tΘ§©¹t+3Θ©Θ§
SΘΫ![]() ΓΝΘ®3©¹tΘ©ΘΫt2©¹6t+9Θ§
ΓΝΘ®3©¹tΘ©ΘΫt2©¹6t+9Θ§
Ήέ…œΥυ ωΘΚ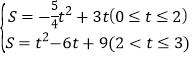 Θ°
Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ